Signal Module I: Definition, Types, and System Interaction

Signal Components: Even and Odd

Problem Statement

Determine the even and odd components of the signal: $x(t) = e^{2t} \cos t$

Key Concepts:

• Even Signal ($x_c(t)$) : Symmetric about the y-axis. Formula: $x_c(t) = \frac{x(t) + x(-t)}{2}$
• Odd Signal ($x_o(t)$) : Symmetric around the origin. Formula: $x_o(t) = \frac{x(t) - x(-t)}{2}$

Solution Steps

1. Define the Components

Given the signal: $x(t) = e^{2t} \cos t$

Transform:

• $x(-t) = e^{-2t} \cos(-t) = e^{-2t} \cos t$

2. Even Component Calculation ($x_c(t)$)

$x_c(t) = \frac{1}{2} \left( e^{2t} \cos t + e^{-2t} \cos t \right)$

Simplification Insight:

• Use the identity for hyperbolic cosine: $\cosh x = \frac{e^x + e^{-x}}{2}$

$x_c(t) = \cos t \cdot \cosh(2t)$

3. Odd Component Calculation ($x_o(t)$)

$x_o(t) = \frac{1}{2} \left( e^{2t} \cos t - e^{-2t} \cos t \right)$

Simplification Insight:

• Use the identity for hyperbolic sine: $\sinh x = \frac{e^x - e^{-x}}{2}$

$x_o(t) = -\cos t \cdot \sinh(2t)$

4. Final Expressions

Even Component:

$x_c(t) = \cos t \cdot \cosh(2t)$

Odd Component:

$x_o(t) = -\cos t \cdot \sinh(2t)$

Additional Insights

Hyperbolic Trigonometric Identities:

• Hyperbolic Cosine ($\cosh x$) : $\cosh x = \frac{e^x + e^{-x}}{2}$

• Hyperbolic Sine ($\sinh x$) : $\sinh x = \frac{e^x - e^{-x}}{2}$

These functions are critical in simplifying the expressions for even and odd components. They are analogous to the regular trigonometric cos and sin but are used in hyperbolic geometry contexts.

Symmetries in Signals:

• Even Symmetry: The function remains the same if $t$ is replaced by $-t$.
• Odd Symmetry: The function changes sign if $t$ is replaced by $-t$.

Understanding these symmetries helps in analyzing signal behaviors in various domains such as frequency analysis.

Extended readings:

Classification of Signals

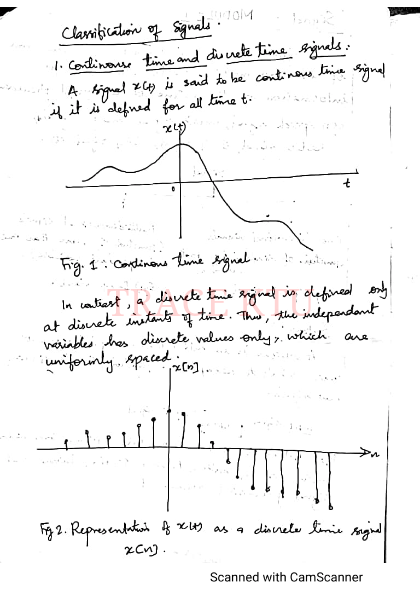
Continuous-Time and Discrete-Time Signals

Continuous-Time Signals

A signal $x(t)$ is said to be a continuous-time signal if it is defined for all time $t$.

• Definition:
  • Continuous-time signals are represented by functions that are defined at every instant. They are usually modeled as smooth waveforms.
• Example:
  • Refer to Fig. 1: The graph shows a continuous-time signal $x(t)$ plotted against time $t$.
• Insight:
  • Continuous signals are analyzed in domains like calculus, where there is an interest in instantaneous values and continuous changes over time.

Discrete-Time Signals

In contrast, a discrete-time signal is defined only at discrete intervals of time. Thus, the independent variable has discrete values only, which are uniformly spaced.

• Definition:
  • Discrete-time signals are sequences of values or samples, typically represented as $x[n]$.
• Example:
  • Refer to Fig. 2: The graph shows the representation of $x[n]$ as a discrete-time signal.
• Insight:
  • Discrete-time signals are central to digital signal processing (DSP), where continuous signals are sampled at discrete intervals for analysis and processing using computers and digital systems.

Additional Information

• Sampling:
  • The process of converting a continuous-time signal into a discrete-time signal by taking samples at regular intervals.
• Nyquist Theorem:
  • A fundamental principle that describes the necessary sampling rate to avoid loss of information when converting a continuous signal to a discrete one.

Understanding the distinction between continuous and discrete signals is crucial in fields like communications, control systems, and digital electronics.

**Extended readings:**
::urlcard[Nyquist–Shannon sampling theorem - Wikipedia]{src="https://en.wikipedia.org/wiki/Nyquist%E2%80%93Shannon_sampling_theorem"}
::urlcard[Sampling in Digital Communication - GeeksforGeeks]{src="https://www.geeksforgeeks.org/sampling-in-digital-communication/"}
::urlcard[3.1 Continuous-time and discrete-time signals - Fiveable]{src="https://library.fiveable.me/bioengineering-signals-systems/unit-3/continuous-time-discrete-time-signals/study-guide/a5iwtfwxONvrgc3h"}


# Signal Module I

![page-1.png](https://psdgfelmelrmwkbhjlza.supabase.co/storage/v1/object/public/images/02f5f3ee-b960-4db3-bbba-b529b54ab73b/3CEH5sToQsv0Ua93V9j2B.png)

## Definition of a Signal
A **signal** is formally defined as a function of one or more variables that conveys information about the nature of a physical phenomenon. 

**Examples include:** 
- Speech signals
- Music signals
- Image signals
- Radar signals
- ECG signals
- EEG signals

**Insight:** Signals can be used to represent or transmit information. They are fundamental in communication systems, medical diagnostics, and digital media.

## Types of Signals

### One-dimensional Signals
- **Description:** Function of a single independent variable.
- **Example:** Speech signals.
  
**Insight:** One-dimensional signals are simplest to analyze and process, commonly represented over time (e.g., audio waveforms).

### Multi-dimensional Signals
- **Description:** Function of more than one independent variable.
- **Example:** Image signals.

**Insight:** Multi-dimensional signals such as images require complex processing techniques, utilizing pixels in multiple dimensions.

## Definition of a System

A **system** is an entity that manipulates one or more signals to accomplish a function, thereby yielding new signals.

```mermaid
graph TD;
    Input_Signal-->System;
    System-->Output_Signal;

Examples include:

• Automatic speech recognition systems
• Communication systems
• Control systems
• Remote sensing
• Biomedical signal processing systems

Insight: Systems process input signals to produce desired outcomes or extract information, crucial in numerous applications such as healthcare and engineering.

Additional Information:

• Control Systems: Used in automation and robotics to maintain desired outputs.
• Biomedical Signal Processing: Involves ECG and EEG signals used for monitoring patient health.

Understanding how signals are processed by systems can enhance the design and functioning of various technologies, from consumer electronics to sophisticated medical equipment.

Señal de Función Impar: Análisis y Descomposición

Función Original y Verificación de Señal Impar

La función dada es: