Kinematics: Key Principles and Galilean Equation Insights
Notes on Kinematics
1. Mișcarea rectilinie uniformă - variația
-
Definiție: Accelerația este constantă.
- Se consideră un mișcător cu accelerație constantă, ceea ce înseamnă că viteza crește sau scade uniform în timp.
-
Formula accelerației:
- Aceasta arată cum viteza se schimbă în funcție de timp, importantă pentru anameneu în problemele de dinamică.
-
Legea vitezei:
- Această formulă este utilă pentru a determina viteza finală a unui obiect în mișcare uniformă.
-
Forma simplificată:
- Utilizabilă dacă se folosește un cronometru pentru a măsura timpul.
-
Operatorul matematic delta (Δ):
- Reprezintă o variație a unei mărimi, important pentru calculul variației în timp sau spațiu.
2. Mișcarea uniform variată - legea vitezei
-
Accelerația calculată ca medie:
-
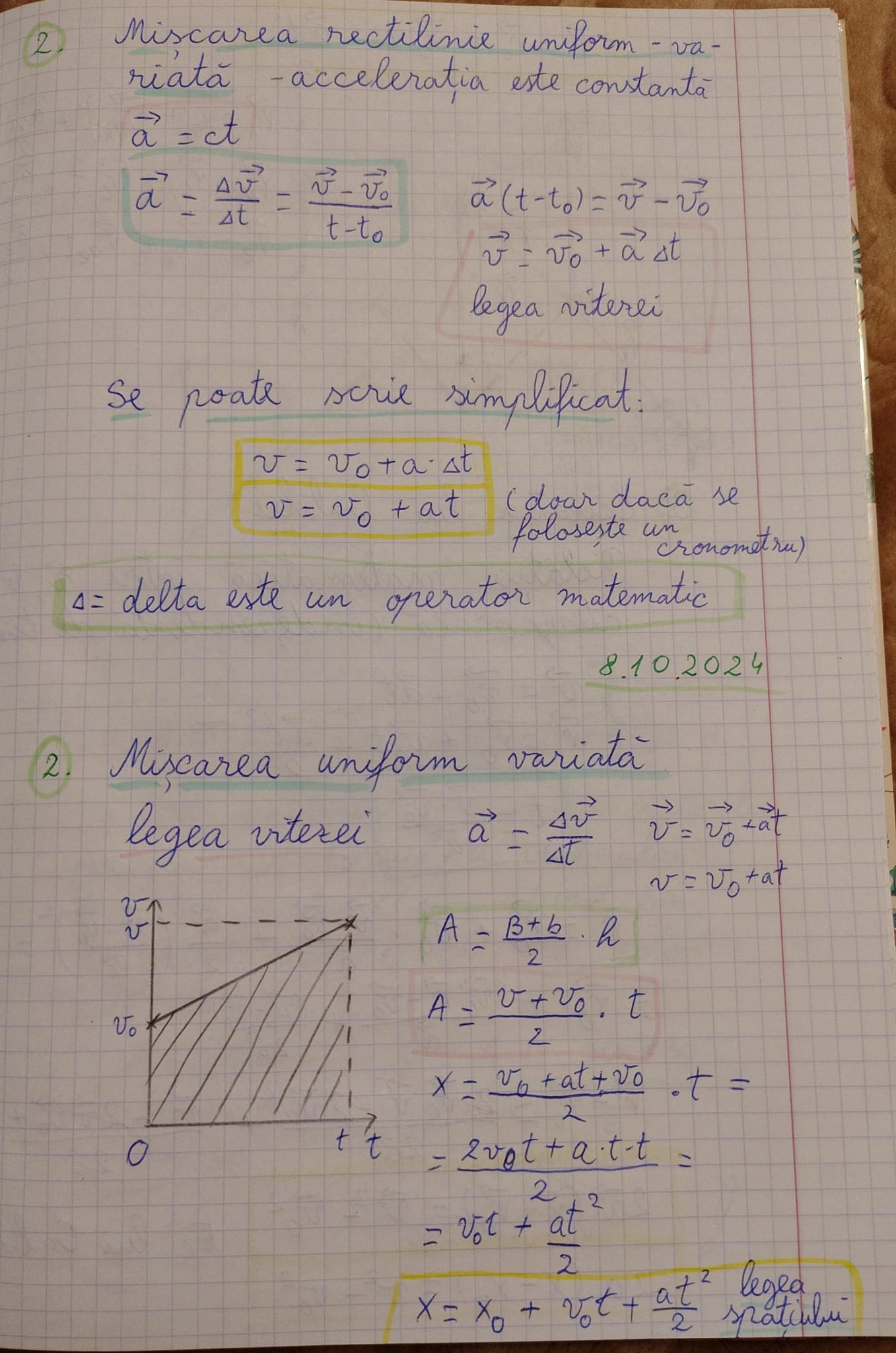
Diagramă viteza-timp:
- Un grafic care arată cum viteza variază în funcție de timp. Aria sub grafic reprezintă distanța parcursă.
-
Formule pentru arnceimea trapezului:
- Aici, și sunt lungimile bazelor trapezului, iar este înălțimea acestuia.
-
Distanța parcursă (X):
- Aceasta este formula generală pentru a determina distanța parcursă de un obiect cu accelerație constantă.
Gânduri finale
Cunoașterea acestor principii fundamentale ale mecanicii este esențială pentru a înțelege mișcarea obiectelor în fizică. Aceste formule nu doar că sunt importante pentru aplicații practice, dar ajută și în dezvoltarea unei gândiri critice în analizarea problemelor de dinamică.
Extended readings:
Ecuația lui Galilei

Introducere
Ecuația lui Galilei descrie mișcarea unui obiect în cadrul mecanicii clasice și se bazează pe principiul observației a lui Galileo despre mișcarea uniform accelerată. Această ecuație este esențială pentru înțelegerea cinematicii.
Relația între variabile
-
Ecuația generală a mișcării
- Unde:
- = poziția finală
- = poziția inițială
- = viteza inițială
- = accelerația
- = timpul
Ideea principală este că poziția unui obiect se poate calcula cunoscând poziția sa inițială, viteza inițială, accelerația și timpul.
- Unde:
-
Componentă pe axe
undefined
Timpul în funcție de viteză
- Formula pentru timpul de mișcare
- Aceasta arată cum timpul de mișcare depinde de variația vitezei și accelerația. Este utilă pentru a estima cât timp va dura un obiect să ajungă la o viteză dată, având în vedere accelerația sa.
Ecuații auxiliare
-
Ecuația de bază
- Aceasta e folosită pentru a determina variația poziției în funcție de timp și accelerație.
-
Ecuație finală
- Această ecuație arată relația dintre schimbarea poziției și variația vitezei, fără a depinde de timp. Este esențială în problemele de mișcare uniform accelerată.
Concluzie
Ecuația lui Galilei este un fundament crucial în studiul mecanicii clasice. Înțelegerea acestor relații permite studenților să abordeze probleme complexe de cinemetică și să aplice conceptele în diverse contexte fizice.
Extended readings: