Note despre vectori și cinematica în fizică

Note despre vectori

1. Înmulțirea unui vector cu un scalar

• Definiție: Fie vectorul $\vec{A}$ și scalarul $n$. Prin înmulțirea vectorului $\vec{A}$ cu scalarul $n$, se obține un vector $\vec{B} = n \cdot \vec{A}$ care are aceeași direcție, sens și punct de aplicare cu vectorul dat, dar cu mărimea de $n$ ori mai mare.
• Importanță: Această operație este esențială în geometria analitică și în fizică, unde scalarii pot reprezenta mărimi precum forța sau masa, iar vectorii reprezintă direcții și magnitudini.

2. Produsul scalar a doi vectori

• Definiție: Fie vectorii $\vec{A}$ și $\vec{B}$. Produsul scalar al celor doi vectori se denotează prin $C = \vec{A} \cdot \vec{B} = |\vec{A}| \cdot |\vec{B}| \cdot \cos \alpha$, unde $\alpha$ este unghiul dintre $\vec{A}$ și $\vec{B}$.
• Utilitate: Produsul scalar este util pentru a determina unghiul dintre vectori și se utilizează frecvent în problemele de fizică și matematică. Un rezultat pozitiv indică faptul că vectorii sunt orientați într-o direcție similară, în timp ce un rezultat negativ indică o orientare opusă.

Tabel de valori pentru sin și cos

• Observații: Tabelul ilustrează valorile funcțiilor trigonometric pentru unghiuri esențiale, ce pot fi folosite pentru a calcula produsul scalar. Aceste relații sunt fundamentale în trigonometrie și au aplicații în diverse domenii științifice.

Extended readings:

Produsul vectorial al două vectori

Definiție

Produsul vectorial a două vectori $\overrightarrow{A}$ și $\overrightarrow{B}$ se notează: $\overrightarrow{C} = \overrightarrow{A} \times \overrightarrow{B}$ Aceasta este o operație care produce un nou vector $\overrightarrow{C}$ din vectorii $\overrightarrow{A}$ și $\overrightarrow{B}$.

Caracteristici

• Mărimea: $C = A \cdot B \cdot \sin \theta$

  • Aici, $C$ reprezintă mărimea vectorului rezultat, $A$ și $B$ sunt mărimile vectorilor inițiali, iar $\theta$ este unghiul dintre aceștia. Această formulă sugerează că pentru a obține un produs vectorial maxim, unghiul $\theta$ trebuie să fie de 90 de grade.

• Direcția:

  • Vectorul $\overrightarrow{C}$ este perpendicular pe planul determinat de $\overrightarrow{A}$ și $\overrightarrow{B}$. Aceasta înseamnă că unghiul dintre vectorul rezultat și fiecare dintre vectorii inițiali va fi de 90 de grade.

• Sensul vectorului:

  • Sensul lui $\overrightarrow{C}$ se determină folosind regula burghiu-lui (screw rule). Aceasta implică:
    • Burghiu în direcția perpendiculară pe planul format de vectori $\overrightarrow{A}$ și $\overrightarrow{B}$ se rotește de la primul vector către al doilea pe calea celui mai scurt drum. Acest lucru înseamnă că direcția este dată de sensul de rotație al burghiu-lui.

• Punctul de aplicare:

  • Punctul de aplicare al vectorului $\overrightarrow{C}$ este comun cu cei doi vectori $\overrightarrow{A} \times \overrightarrow{B}$, ceea ce înseamnă că vectorul rezultat își are originea în același punct ca și cei doi vectori inițiali.

Observații suplimentare

• Produsul vectorial nu este comutativ; adică: $\overrightarrow{A} \times \overrightarrow{B} \neq \overrightarrow{B} \times \overrightarrow{A}$ De fapt, direcția vectorului rezultat va fi opusă atunci când schimbăm ordinea în care efectuăm produsul vectorial. Acest aspect este esențial de reținut deoarece poate influența semnificația fizică a calculului.

Extended readings:

Mecanică - Cinematică

Definiție

Cinematica este partea mecanicii care se ocupă cu studiul mișcării corpurilor fără a ține seamă de cauzele acesteia.

• Observație: Aceasta înseamnă că cinematică analizează doar descrierea și comportamentul mișcării, fără a considera forțele care o provoacă.

G. Galilei

• Importanță : Galilei este un fondator al cinematicii moderne, având contribuții esențiale în înțelegerea mișcării.

Modele Fizice

Cinematica folosește concepte numite modele fizice, care sunt simplificări ale realității.

• Reflecție: Modelele fizice sunt esențiale pentru a face simulări și predicții în fizică, ajutând la reducerea complexității fenomenelor naturale.

Sistemul de Referință (SR)

Definiție

Sistemul de referință este un corp de referință redus mental la dimensiunile unui punct căruia i se atașează o riglă pentru măsurarea distanțelor și un ceasornic pentru măsurarea timpului.

• Clarificare: Acest sistem permite observarea și măsurarea pozițiilor obiectelor în mișcare. Fără un sistem de referință clar, este imposibil să definim mișcarea sau să comparăm diferite ierarhii de mișcare.

Concepții Importante

• Reducerea mentală : Ideea de a reduce complexitatea unui sistem fizic pentru a facilita analiza.
• Funcția observatorului: Este important ca observatorul să fie conștient de sistemul de referință ales, deoarece poate influența percepția asupra mișcării.

Concluzie

Înțelegerea cinematicei și a sistemelor de referință este fundamentală pentru studiul fizicii, deoarece acestea oferă cadrul pentru analiza mișcării și interacțiunilor între corpuri.

Extended readings:

Reprezentarea Sistemului de Referință

• Sistem de 3 Dreapte Concurente

  • Se reprezintă printr-un sistem de 3 dreapte concurente care descrie spațiul cu 3 dimensiuni.
  • Este important de înțeles cum aceste dreapte interacționează pentru a defini un cadru de referință.

• Originea Sistemului de Referință (O)

  • Corpul de referință se află la intersecția celor 3 dreapte și este numit originea sistemului de referință.
  • Această origine este crucială pentru determinarea poziției și mișcării obiectelor în spațiu.

• Determinarea Mișcării

  • Sistemul de referință se folosește pentru a determina starea de mișcare a unui corp în raport cu acesta.
  • Aceasta implică observația schimbărilor în poziție și orientare a corpului în raport cu originea sistemului.

• Schimbarea Pozicii și Mișcare

  • Un corp se află în mișcare dacă își schimbă poziția față de originea sistemului de referință.
  • Mișcarea este, în esență, o schimbare de poziție în timp, care poate fi observată prin schimbări în direcție sau viteză.

• Situații Multiple de Mișcare

  • Aceeași corp poate fi simultan în diferite stări de mișcare în raport cu diferite sisteme de referință.
  • Acest concept este esențial în fizică, deoarece ajută la explicarea relativității mișcării.

• Exemplu Practic

  • De exemplu, un tren care se mișcă pe o linie de cale ferată poate fi considerat în repaus în raport cu platforma stației, dar în mișcare față de un observator pe marginea căii ferate.

Aceste note subliniază importanța definirii adecvate a sistemelor de referință pentru a înțelege mișcarea și interacțiunile dintre obiecte.

Extended readings:

Notițe despre relativitatea mișcării

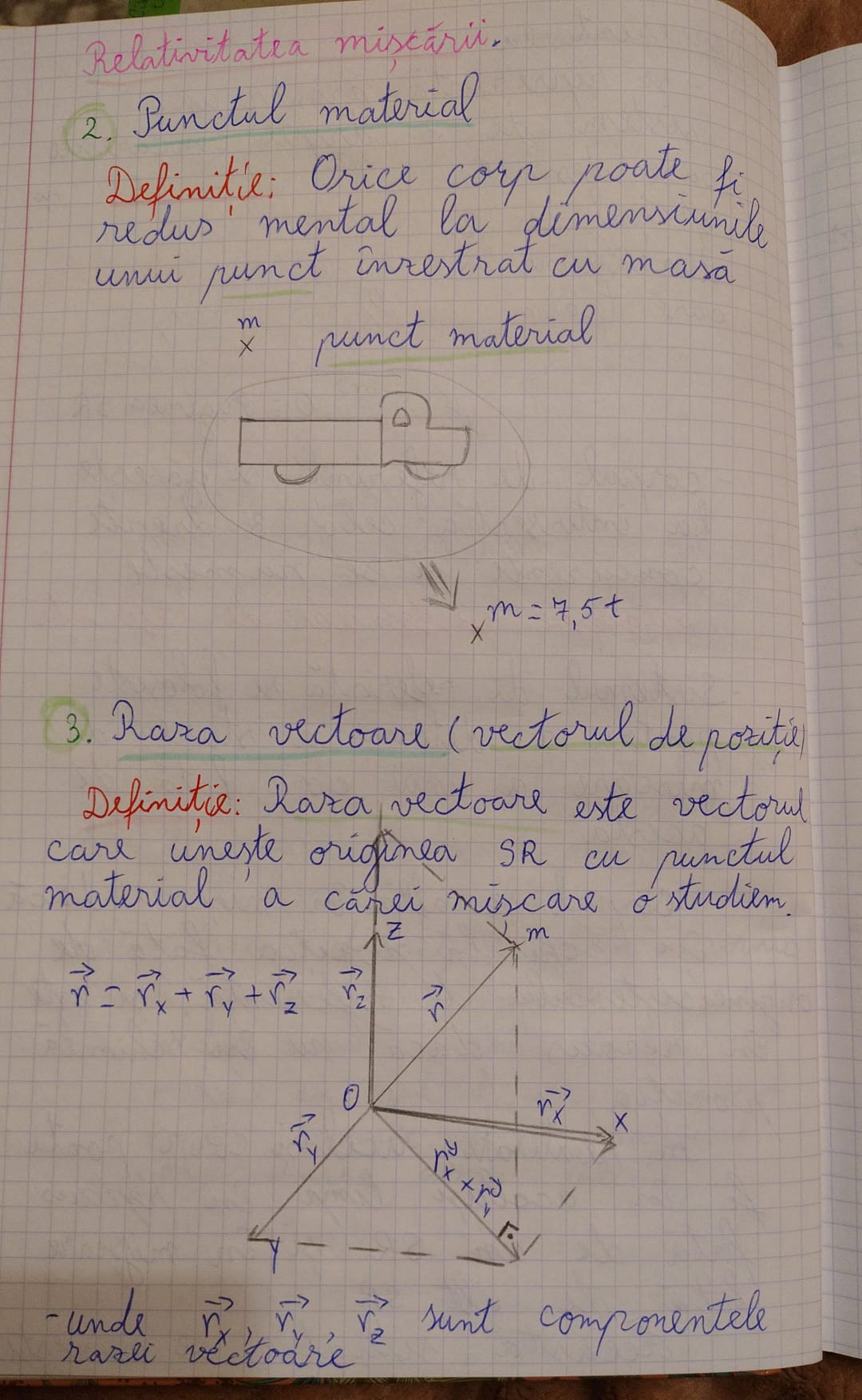
1. Punctul material

• Definiție: Orice corp poate fi redus mental la dimensiunile unui punct înserat cu masă.
  • Explicație: Conceptul de „punct material” este utilizat în fizică pentru a simplifica analiza mișcării, prin considerarea unui obiect ca având doar masă, fără dimensiuni. Acesta permite aplicarea legilor fizicii mai ușor, fără a lua în calcul dimensiunile reale ale corpului.
  • Exemplu: Un automobil poate fi reprezentat ca un punct material în multe calcule de dinamică, atâta timp cât dimensiunile sale nu influențează rezultatul dorit.

2. Raza vectorială (vectorul de poziție)

• Definiție: Raza vectorială este vectorul care unește originea sistemului de referință (SR) cu punctul material a cărei mișcare o studiem.
  • Explicație: Raza vectorială este esențială în studierea mișcării, deoarece reflectă poziția unui obiect în raport cu un punct de referință, permițând calcularea distanței și direcției mișcării.
  • Notare: Se poate reprezenta ca un vector $\vec{r} = \vec{r}_x + \vec{r}_y + \vec{r}_z$, unde $\vec{r}_x$, $\vec{r}_y$, și $\vec{r}_z$ sunt componentele vectorului pe axele x, y, și z. Acest lucru conține informații despre direcția și magnitudinea mișcării.

• Importanță: Înțelegerea razei vectoriale este importantă pentru analiza mișcării în trei dimensiuni, fiind un concept de bază în mecanica clasică și în alte domenii ale fizicii.

Extended readings:

::urlcard[Andrei Popovici - Cursuri de teoria relativitatii [Lectures on Theory of ...]{src="https://www.academia.edu/105672795/Andrei_Popovici_Cursuri_de_teoria_relativitatii_Lectures_on_Theory_of_Relativity_545_pp_"}