**Title: Understanding Electric Vehicles and Basic Electrical Concepts**

Voltage, Current, Resistance, and Ohm's Law - SparkFun Learn

study.com

Ohm's Law | Relationship Between Voltage, Current & Resistance

Voltage, Current, Resistance, and Ohm's Law - SparkFun Learn

Ohm's Law

Definition and Origin
- Ohm's Law is named after Mr. Ohm, who defined the relationship among Current, Voltage, and Resistance.
  - Thoughts: This law is fundamental in electrical engineering and physics, serving as a building block for understanding electric circuits.
Basic Electrical Units
- The law encompasses three basic electrical units: Current (I), Voltage (V), and Resistance (R).
  - Additional Information:
    - Current (I) is measured in Amperes (A).
    - Voltage (V) is measured in Volts (V).
    - Resistance (R) is measured in Ohms (Ω).
Applications
- These principles apply to both Alternating Current (AC) and Direct Current (DC).
  - Thoughts: Understanding the application of Ohm's Law in AC and DC is crucial, as they behave differently in circuits.
Types of Current
- Alternating Current: Changes with respect to time.
- Direct Current: Remains constant.
  - Additional Information:
    - AC is commonly used in household power supplies, while DC is found in batteries and electronics.
Summary of Ohm's Law
- The relationship can be expressed mathematically as V = I × R, where:
  - V = Voltage (in Volts)
  - I = Current (in Amperes)
  - R = Resistance (in Ohms)
  - Thoughts: This formula highlights the direct proportionality between current and voltage, and the inverse relationship with resistance. Understanding this helps in designing and analyzing electrical circuits.

Reference:

www.ncbi.nlm.nih.gov

Ohms Law - StatPearls - NCBI Bookshelf

Ohm's Law - Statement, Formula, Solved Examples, Verification, FAQs

Ohm's law - Wikipedia

byjus.com

Ohm's Law

Definition: Ohm's Law states that the current flowing through a conductor between two points is directly proportional to the potential difference (voltage) across the two points, provided the physical conditions, like temperature, remain constant.
- Thoughts: This law is foundational in electrical engineering and physics, helping to understand how electrical circuits operate. It implies that if the voltage increases while resistance remains the same, the current will also increase.
Mathematical Representation:
- $I \propto V$ (Current is proportional to Voltage)
- $I = \frac{1}{R} \cdot V$ (Current equals Voltage divided by Resistance)
- $V = IR$ (Voltage equals Current multiplied by Resistance)
- Thoughts: Understanding these equations is crucial for solving problems in circuits. For example, if you know two of the parameters (voltage, current, resistance), you can easily calculate the third.
Variables Defined:
- $V$ = Voltage (Volts)
- $I$ = Current (Amperes)
- $R$ = Resistance (Ohms)
- Additional Info: Each of these units is essential for analyzing and designing electrical systems. Voltage is the driving force; current is the flow of charge, and resistance opposes that flow.
Application: Ohm's Law can be used in various applications, including calculating the right resistor for a circuit, understanding how batteries work, and analyzing complex circuits in electrical engineering.
- Thoughts: Practically applying Ohm's Law helps troubleshoot electrical problems and design efficient electrical systems. Knowing how to manipulate and measure these values is vital for anyone working in technology.
Caveat: Ohm's Law only applies to ohmic materials (materials that follow this linear relationship between voltage and current). Non-ohmic materials and components, like diodes or transistors, do not obey Ohm's Law in a simple way.
- Thoughts: Understanding the limitations of Ohm's Law is crucial for advanced circuit design where non-linear components are involved.

Reference:

study.com

Ohm's Law | Relationship Between Voltage, Current & Resistance

What is Ohm's Law: Definition, Formula, Graph & Limitations

Ohm's law - Wikipedia

www.geeksforgeeks.org

Notes on Voltage and Current

Voltage

Definition: Voltage is the energy required to move a charge from one point to another.
Units: Measured in Volts (V).
Measurement Tool: A Voltmeter is used to measure voltage.
Formula: According to Ohm’s law, voltage is calculated as $V = IR$ $V = I R$ , where:
- $V$ = Voltage
- $I$ = Current
- $R$ = Resistance

Thoughts: Understanding voltage is crucial for basic electrical engineering and electronics. It can be thought of as the "push" that drives electric charges through a circuit.

Current

Definition: Current is the flow of charge in a conductor.
Units: Measured in Amperes (A).
Measurement Tool: An Ammeter is used to measure current.
Formula: From Ohm’s law, current can be determined using $I = \frac{V}{R}$ $I = \frac{V}{R}$ , where:
- $I$ = Current
- $V$ = Voltage
- $R$ = Resistance

Thoughts: Current is a fundamental concept in electricity, essential for operating electronic devices. It indicates the amount of flow of electric charge and is directly related to the voltage and resistance present in the circuit.

Summary

Understanding the relationship and definitions of voltage and current is vital for anyone studying electrical systems, as they play key roles in circuit design and functionality. The formulas derived from Ohm's law provide the foundational principles for calculating electrical properties in circuits.

Reference:

study.com

Ohm's Law | Relationship Between Voltage, Current & Resistance

Ohm's Law - How Voltage, Current, and Resistance Relate

Voltage, Current, Resistance, and Ohm's Law - SparkFun Learn

Notes on Resistance in Electric Circuits

Definition of Resistance
Resistance is the measure of opposition to the current flow in an electric circuit. This concept is crucial for understanding how electric components behave when connected in a circuit. It helps in designing circuits for specific applications by allowing us to control the amount of current flowing.
Unit of Measurement
Resistance is measured in Ohms (Ω). Understanding this unit is fundamental since it helps in standardizing measurements across different electrical components.
Ohm's Law
The relationship between voltage (V), current (I), and resistance (R) is defined by Ohm's Law: $R = \frac{V}{I}$ This formula indicates that resistance is calculated by dividing the voltage across a component by the current flowing through it. It is essential for solving circuit problems and understanding how changing one variable affects the others.
Effect of Resistance on Current
Higher resistance results in lower current flow and vice versa. This inverse relationship is key in applications like resistor design in circuits, where control over current is necessary to protect delicate components from damage.
Example Calculation
The image provides an example of calculating current (I) using the given voltage (9 V) and resistance (3 kΩ):
$I = \frac{V}{R} = \frac{9}{3} = 3 \text{ mA}$$ This calculation exemplifies how to apply Ohm's Law practically, allowing users to predict how much current will flow based on known values of voltage and resistance.$

Summary Table

Parameter	Value
Voltage (V)	9 V
Resistance (R)	3 kΩ
Current (I)	3 mA

This table succinctly summarizes the essential components from the example, making it easy to reference for calculations or further study.

Reference:

ohmslaw.eu

Calculate Ohm's Law: V, 3kΩ, 3mA

Series Circuits and the Application of Ohm's Law

electronics.stackexchange.com

ohms law - How to understand this circuit?

Direct Current (DC) in Electrical and Power Electronics

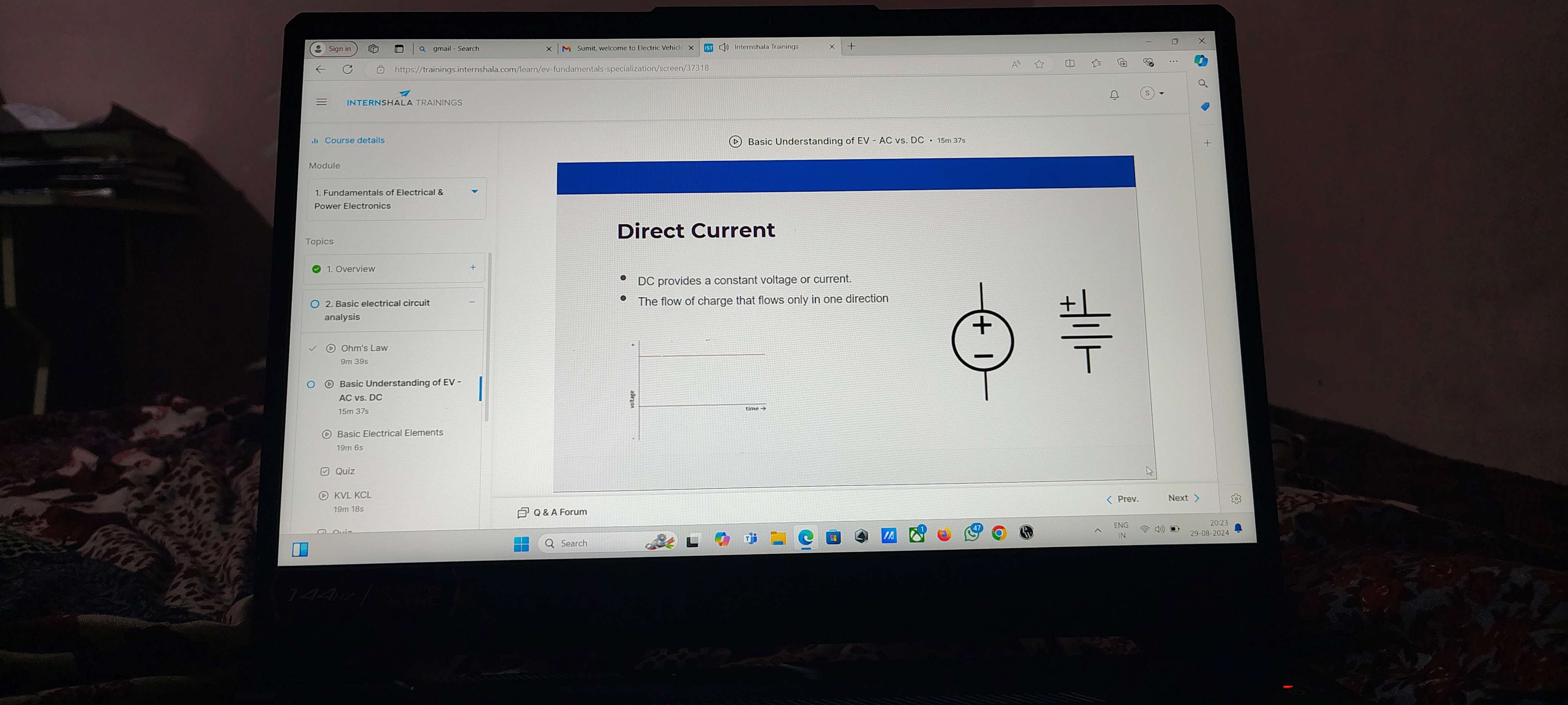
Overview of Direct Current

Definition: Direct Current (DC) provides a constant voltage or current, meaning the flow of electric charge remains steady over time.
- Thoughts: Unlike alternating current (AC), where the current changes direction periodically, DC is more predictable and stable, making it ideal for many applications.
- Additional Information: Common sources of DC include batteries, solar cells, and DC power supplies.

Current Flow in DC

Characteristics: The flow of charge in DC flows in only one direction.
- Thoughts: This unidirectional flow is crucial for devices that require a steady supply, such as electronic circuits and motors.
- Additional Information: Understanding the direction of current flow is vital for circuit design and analysis, especially when applying laws such as Kirchhoff's Voltage Law (KVL) and Kirchhoff's Current Law (KCL).

Visual Representation

Graph: A simple graph depicting current (or voltage) against time, showing a constant level indicates the steady output that characterizes DC.
- Thoughts: Graphs are helpful in visualizing the relationships between electrical parameters and time. This can assist in understanding the system's behavior over time.
- Additional Information: This contrast in graphs of DC and AC (which typically oscillates over time) can clarify their differing behaviors in circuits.

Conclusion

Understanding the fundamentals of direct current, including its characteristics and applications, is essential for anyone studying electrical and power electronics. The stability of DC makes it a foundational concept in electrical engineering.

Reference:

unacademy.com

Specific Characteristics Of Direct Current - Unacademy

Characteristics and Applications of DC (Direct Current) Signals

www.geeksforgeeks.org

Direct Current - Working, Principle, Types and Components

Direct Current

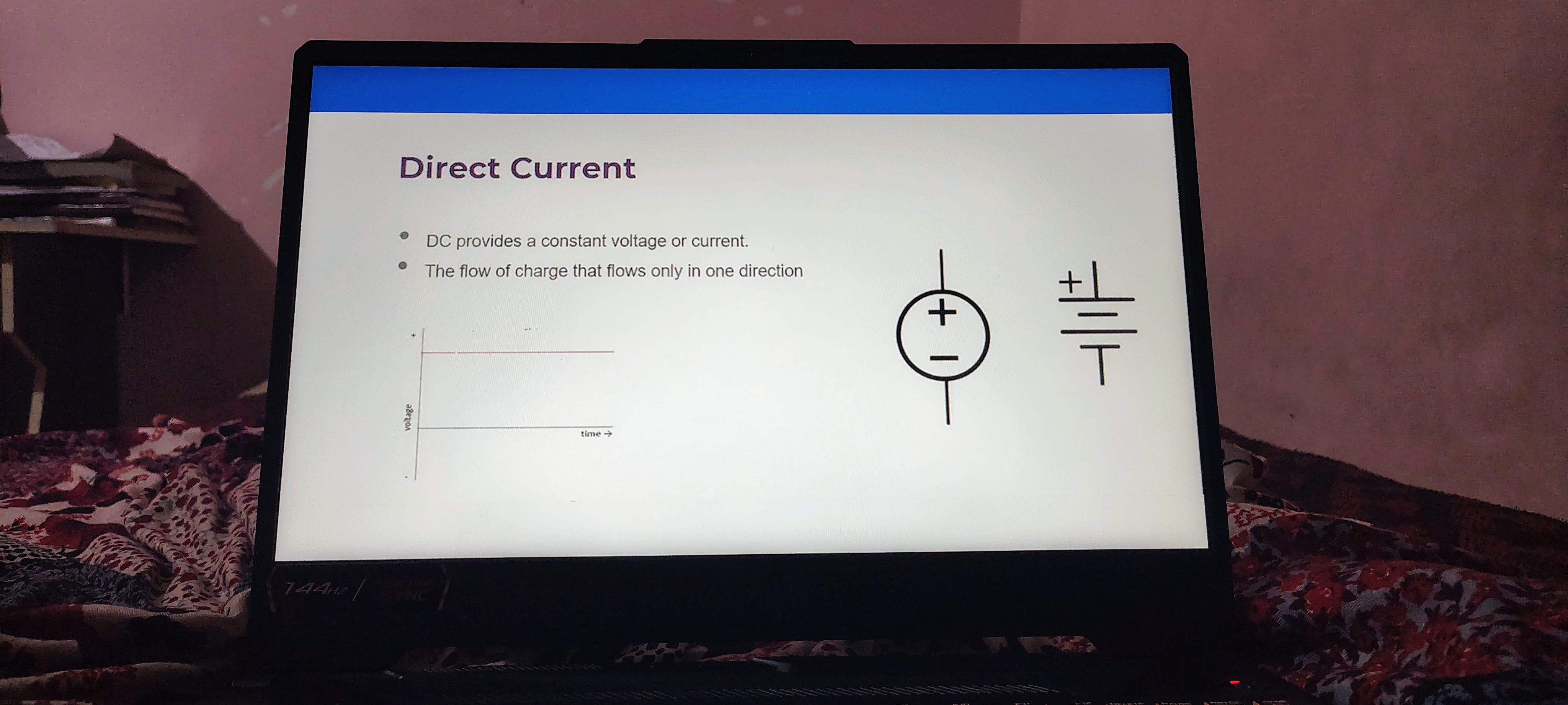
DC provides a constant voltage or current.
- Direct Current (DC) is characterized by a constant voltage and current over time. Unlike alternating current (AC), which changes direction periodically, DC maintains a steady flow. This stability makes DC suitable for low-voltage applications like batteries and electronic circuits.
The flow of charge that flows only in one direction.
- In DC, electric charge moves in a single direction, typically from the positive terminal to the negative terminal. This unidirectional flow is essential in many electronic devices; for instance, transistors and integrated circuits require DC for proper operation.
Graphical Representation of DC:
- The image displays a simplistic graph indicating that voltage remains constant over time, which illustrates the principle of DC being stable without fluctuation, contrasting with AC, where the voltage varies sinusoidally.
Symbols for direct current:
- The symbols shown on the screen represent components in a DC circuit. The first symbol is a battery, which is a common source of DC, while the second symbol represents a DC circuit. Understanding these symbols is crucial for reading and designing electrical schematics.

Additional Thoughts:

DC is prevalent in today’s technology, notably in renewable energy systems, such as solar panels and electric vehicles, which often rely on DC for storage in batteries.
Understanding direct current is foundational for anyone studying electrical engineering, as it forms the basis for more complex systems and applications.

Reference:

eepower.com

Basic DC Circuit Theory - Voltage, Current, Energy, and Power

Voltage and Current | Basic Concepts Of Electricity - All About Circuits

www.geeksforgeeks.org

Direct Current - Working, Principle, Types and Components

Alternating Current (AC)

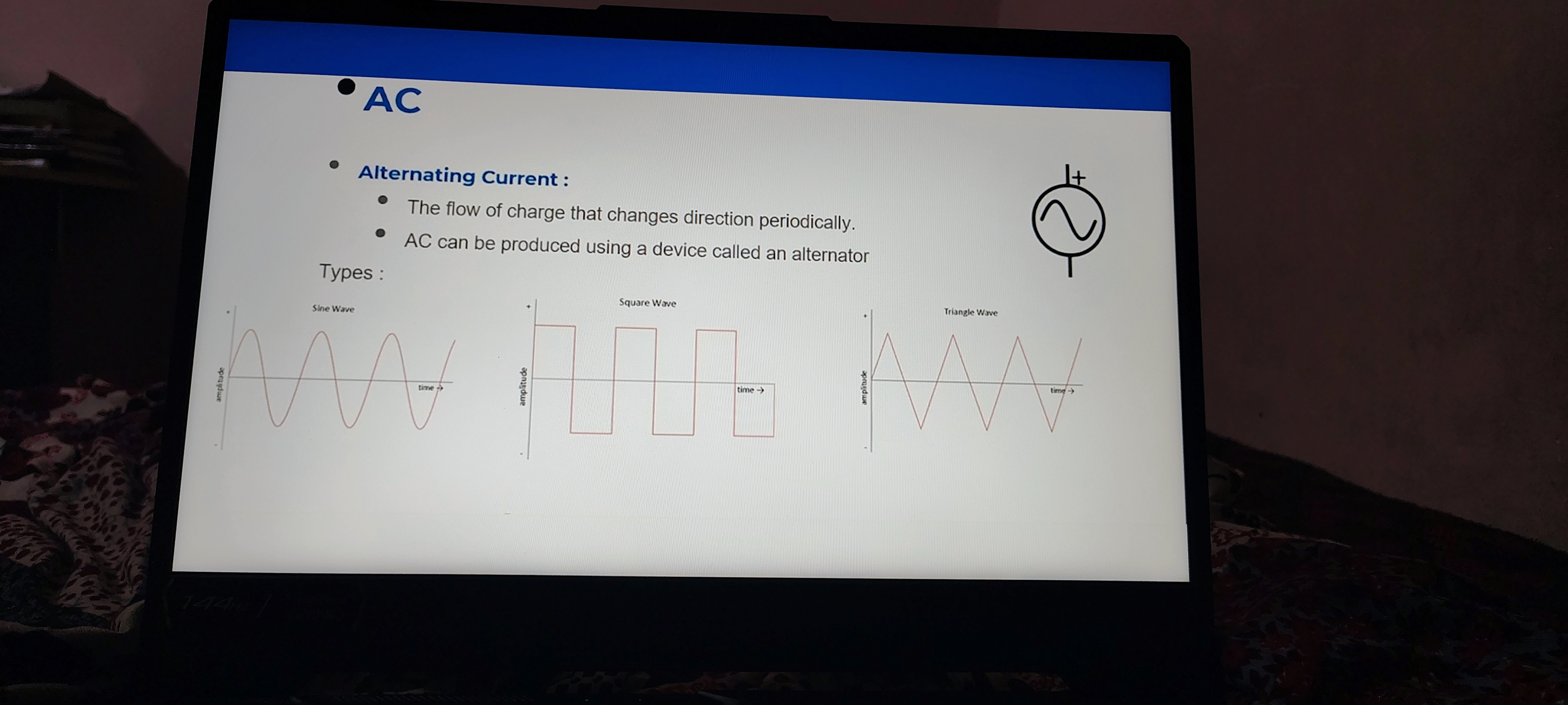
Definition

Alternating Current (AC) : The flow of electric charge that changes direction periodically.
- Additional Information: Unlike direct current (DC), which flows in one direction, AC is commonly used for power supply in homes and industries due to its efficiency in transporting electricity over long distances.

Generation of AC

Production: AC can be produced using a device called an alternator.
- Thoughts: Alternators are crucial in power generation and are widely used in power plants and automobile engines to supply electricity.

Types of AC Waves

AC can take different waveforms, the common types include:

Wave Type	Description
Sine Wave	Characterized by a smooth, periodic oscillation; this is the most common form and ideal for AC power.
Square Wave	Contains abrupt transitions; it switches levels sharply, often used in digital electronics.
Triangle Wave	Features a linear rise and fall; it is often used in sound synthesis and signal processing.

Summary of Wave Types

Sine Wave: Ideal for electrical power transmission; represents the purest form of AC.
Square Wave: Useful in digital circuits where a binary signal is needed.
Triangle Wave: Provides a linear transition, useful in both music synthesis and as a reference signal in various applications.

These various waveforms highlight the versatility of AC in different applications, making it a fundamental concept in electronics and electrical engineering.

Reference:

AC Waveform and AC Circuit Theory of Sinusoids

AC Waveforms | Basic AC Theory | Electronics Textbook

Alternating current - Wikipedia

AC Generation Notes

Voltage and Frequency in India:
- In India, the standard voltage is 240 V and the frequency is 50 Hz.
- Understanding these specifications is crucial for electrical engineers and technicians when designing and maintaining electrical systems to ensure compatibility with devices and safety regulations.
AC Generation:
- At the generation level, electricity is produced as Alternating Current (AC) only.
- AC is preferred for power distribution because it can be easily transformed to different voltage levels, allowing for efficient long-distance transmission. This ability to step up or step down voltage is crucial for minimizing energy losses during transmission.
Illustration Description:
- The image depicts a basic diagram illustrating the process of AC generation.
- It likely shows components such as a coil, magnets, or other electrical elements that are fundamental in the generation of AC power. This visual representation can help in understanding how magnetic fields and coils interact to produce electrical energy.

Overall, these notes emphasize the importance of understanding the basic principles of AC electricity, especially in relation to its generation and distribution within the power grid.

Reference:

Why is India's frequency maintained in 50 Hz only? - Quora

Why is the frequency of an AC current in India 50 Hertz ... - Quora

The frequency of AC main is 50 hz in India, wheareas 60Hz in US ...

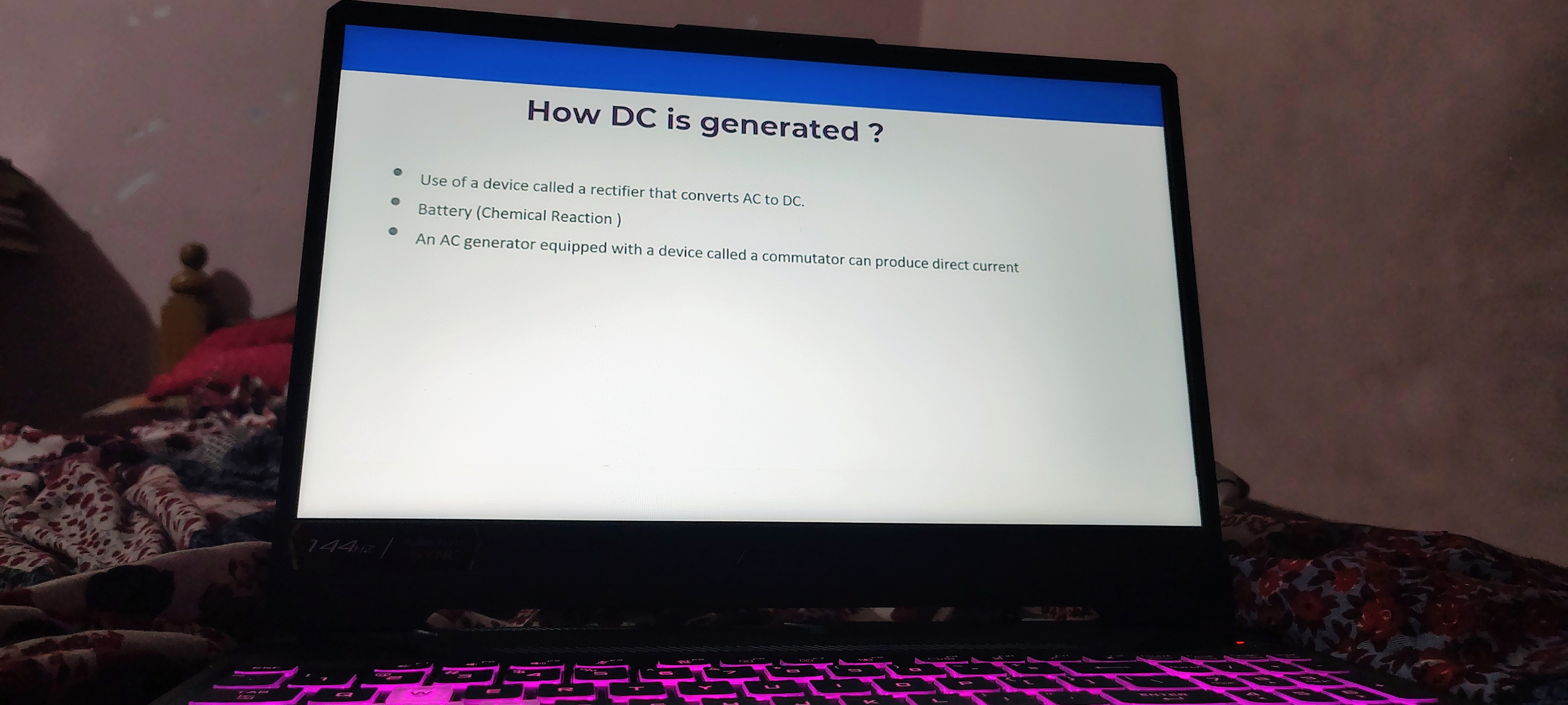
How DC is Generated?

Use of a device called a rectifier that converts AC to DC.
- A rectifier is an essential component in power electronics. It allows alternating current (AC), which changes direction periodically, to be converted into direct current (DC) that flows consistently in one direction. This conversion is crucial for powering devices that require a stable voltage, such as appliances and electronics.
Battery (Chemical Reaction)
- Batteries produce DC voltage through electrochemical reactions. In a battery, chemical energy is transformed into electrical energy. This is why batteries deliver a steady voltage and current output until their chemical reactants are depleted, making them a reliable source of DC power.
An AC generator equipped with a device called a commutator can produce direct current.
- An AC generator, typically producing alternating current, can be modified to produce DC by incorporating a commutator. The commutator ensures that the output current flows in a single direction, converting the AC produced by the generator into DC. This method is particularly useful in applications where a consistent voltage is needed.

Reference:

Alternating Current (AC) vs. Direct Current (DC) - SparkFun Learn

How is DC (Direct Current) generated? - Quora

How is a DC current produced in a generator? - Quora

AC vs DC

AC	DC
AC is safe to transfer longer distances even between two cities and maintain the electric power	DC cannot travel for a very long distance. It loses electric power.
The rotating magnets cause the change in the direction of electric flow.	The steady magnetism makes DC flow in a single direction.
The frequency of AC is dependent upon the country. But, generally, the frequency is 50 Hz or 60 Hz.	DC has no frequency of zero frequency.
In AC, the flow of current changes its direction backwards periodically.	It flows in a single direction steadily.
Electrons in AC keep changing their directions – backward and forward	Electrons only move in one direction – that is forward.
Home Appliances, Commercial Usage	Electronics

Notes

AC (Alternating Current) :
- Transfer over Long Distances: AC is effective for long-distance power transmission due to its ability to maintain voltage levels high, which reduces energy loss over distances. This is crucial for the power grid infrastructure.
- Frequency Dependence: The operational frequency of AC varies globally (50 Hz in Europe and 60 Hz in North America). Understanding the frequency standard is vital for electrical compatibility in devices and infrastructure.
- Direction Change: The alternating nature means AC switches direction periodically, which can be beneficial for certain applications but also complicates design considerations for electrical devices.
- Applications: Commonly used in residential and commercial applications due to its efficiency in distribution.
DC (Direct Current) :
- Distance Limitation: While DC is less effective for long distances compared to AC, it serves well in small-scale applications such as batteries and electronic devices. Advances in technology like HVDC (High Voltage Direct Current) are improving its long-distance efficiency.
- Steady Flow: DC provides a constant voltage which is necessary for sensitive electronic components, making it ideal for electronics.
- Unique Characteristics: DC has no frequency, which simplifies analysis for circuits that are purely electronic as no alternating behavior needs to be considered.
- Applications: Primarily found in electronic devices (like smartphones and laptops) and renewable energy systems (like solar panels).

Conclusion

Understanding the differences between AC and DC is crucial for applications ranging from everyday household electricity to complex electronic systems. This knowledge assists in selecting the correct type of current for specific needs, ensuring efficiency and compatibility in electrical engineering.

Reference:

byjus.com

Difference Between AC And DC - BYJU'S

zendure.com

DC vs AC: Understand the Differences and Their Applications

Alternating Current (AC) vs. Direct Current (DC) - SparkFun Learn

Basic Electrical Components

Introduction to Electrical Components

Definition: Electrical components are electronic parts that can be connected to create electronic circuits. They have specific functions and behaviors depending on their design.
Importance: Understanding these components is crucial for anyone studying electronics or engaging in electrical engineering, as they form the basis of circuit design and functionality.

Common Electrical Components

Resistor
- Function: Limits current flow and divides voltages in a circuit.
- Thoughts: Essential in controlling the amount of current in various branches of a circuit, preventing damage to components that could be subjected to too high of a current.
Capacitor
- Function: Stores and releases electrical energy in a circuit.
- Thoughts: Helpful in smoothing out fluctuations in voltage and providing bursts of energy when needed, such as in power supplies and audio equipment.
Inductor
- Function: Stores energy in a magnetic field when electrical current passes through it.
- Thoughts: Used in various applications, like filtering in power supplies and tuning in radio circuits, emphasizing its role in controlling current changes over time.
Diode
- Function: Allows current to flow in one direction only, protecting circuits from reverse current.
- Thoughts: Fundamental in rectifying circuits (converting AC to DC), highlighting their necessity in power supply designs.
Transistor
- Function: Acts as a switch or amplifier in a circuit.
- Thoughts: Vital in modern electronic devices; understanding their operating principles is essential for developing complex circuits, especially in computing and signal processing.

Conclusion

The knowledge of basic electrical components and their functionalities is crucial for building and analyzing electronic circuits. Mastery of these elements forms the foundation for advanced studies in electronics and electrical engineering.

Resistor Overview

Definition

The resistor is a passive electrical component that creates resistance in the flow of electric current.
- Thoughts: Understanding resistance is crucial for managing electrical circuits effectively. It allows for controlling current flow.

Effect of a Capacitor

The effect of a capacitor is known as resistance.
- Additional Information: Capacitors and resistors are foundational components in electronics. While a resistor restricts current, a capacitor stores electric charge.

Symbols of Resistors

Type	Symbol
Fixed Value Resistor (IEC)
Fixed Value Resistor (IEEE)
Variable Resistor (Potentiometer)
Variable Resistor (Rheostat)
Light Dependent Resistor (LDR)

Thoughts: Recognizing the symbols used for different types of resistors is essential for reading and interpreting electronic schematics.

Characteristics of Resistors

Resistors are electronic components that have a specific, never-changing electrical resistance.
- Additional Information: Different types of resistors serve various functions, such as adjusting voltage levels or limiting current flow.

Formulas Related to Resistors

Unknown Values and Formulas

Unknown Value	Formula
Voltage	$V = I \times R$
Current	$I = \frac{V}{R}$
Resistance	$R = \frac{V}{I}$
Power	$P = V \times I$ or $P = \frac{V^2}{R}$ or $P = I^2R$
Heat	$H = I^2RT$

Thoughts: Mastery of these formulas can simplify problem-solving in electrical engineering and facilitates circuit analysis.
Additional Information: These formulas are fundamental in calculating how various resistors will behave in a circuit, aiding in designing and optimizing electrical systems.

Reference:

www.jakelectronics.com

Resistor Basics: Resistor Symbol - JAK Electronics

Beginners Guide to Passive Devices and Components

Resistor - Wikipedia

Types of Resistor

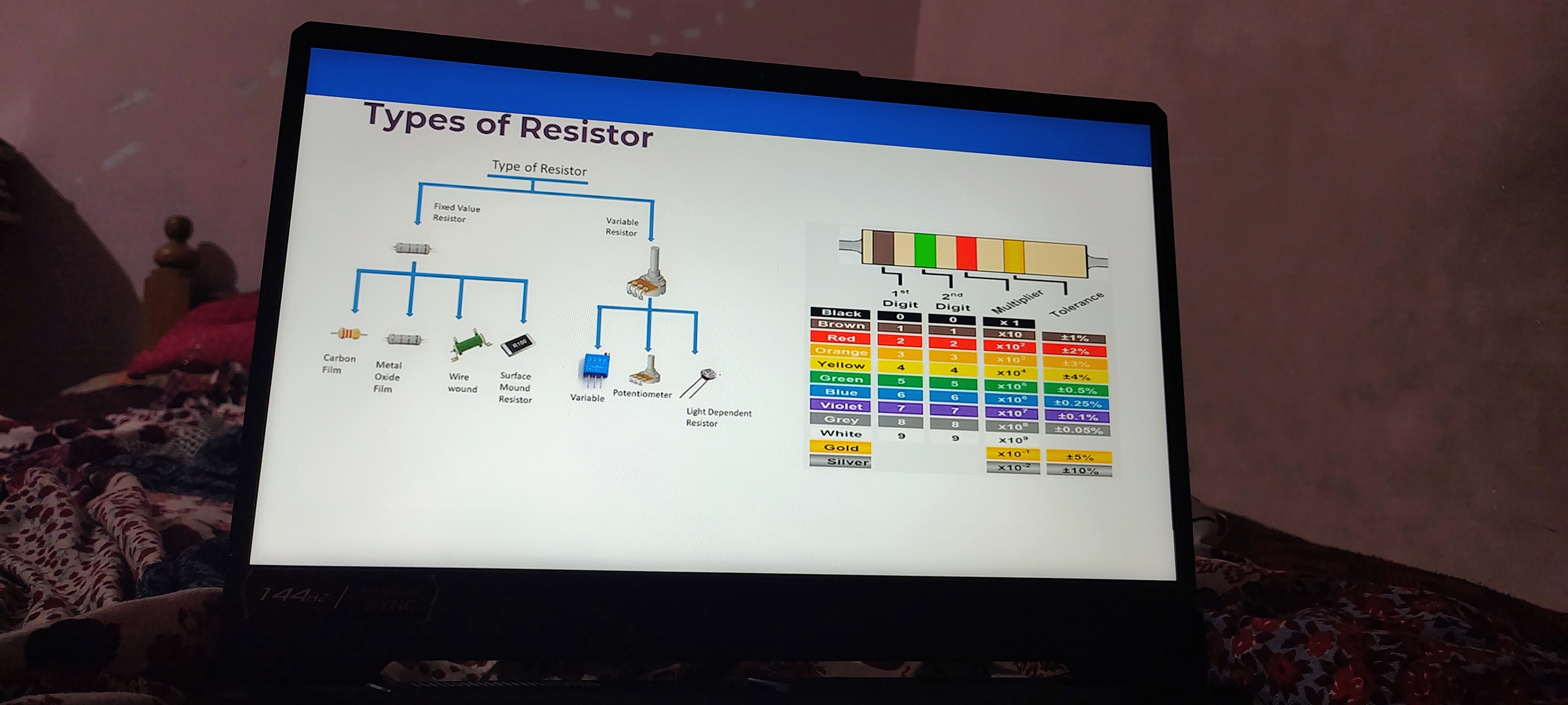
Overview

The image provides an overview of different types of resistors and their classifications. It categorizes resistors into fixed value and variable resistors, along with examples of each type. Understanding these resistors is crucial for anyone working in electronics or electrical engineering.

Fixed Value Resistors

Carbon Film Resistor:
- Commonly used for their stability and low cost.
- Suitable for general-purpose applications.
Metal Oxide Film Resistor:
- Known for higher stability and tolerance.
- Often used in applications requiring precision.
Wire Wound Resistor:
- Made by winding a metal wire around a core.
- Used in high power applications due to their ability to dissipate heat.
Surface Mount Resistor:
- Designed for mounting directly onto the surface of PCBs.
- Popular in modern electronics due to minimizing space and weight.

Variable Resistors

Variable Resistor:
- Allows for adjustable resistance in a circuit.
- Commonly used in applications like volume controls.
Potentiometer:
- A type of variable resistor with three terminals.
- Adjusts voltage output in a circuit and is widely used in audio equipment.
Light Dependent Resistor (LDR) :
- Resistance varies with light intensity.
- Utilized in light-sensitive applications like automatic lighting systems.

Resistor Color Code

The image also includes a resistor color code chart, which helps identify the resistance and tolerance of a resistor based on its color bands. Here’s the extracted information in table format:

Color	1st Digit	2nd Digit	Multiplier	Tolerance
Black	0	0	x10^0	±1%
Brown	1	1	x10^1	±1%
Red	2	2	x10^2	±2%
Orange	3	3	x10^3	±2%
Yellow	4	4	x10^4	±5%
Green	5	5	x10^5	±0.5%
Blue	6	6	x10^6	±0.25%
Violet	7	7	x10^7	±0.1%
Grey	8	8	x10^8	±0.05%
White	9	9	x10^9	±10%
Gold	-	-	x10^-1	±5%
Silver	-	-	x10^-2	±10%

Conclusion

These notes summarize the types of resistors and their characteristics, including how to determine their values using the color code method. This information is fundamental for practical applications in electronics, especially when designing or troubleshooting circuits.

Reference:

Resistor Colour Code and Resistor Tolerances Explained

www.tutorialspoint.com

Resistor Types and Color Code - Tutorialspoint

eepower.com

Resistor Color Code | Resistor Standards and Codes - EEPower

Capacitor Overview

Definition

Capacitor: A device that stores electrical energy in an electric field.
- Thoughts: Capacitors are key components in many electronic circuits, as they can release energy quickly when needed and are essential for filtering and managing power supply.

Characteristics

Passive Electronic Component: Does not require external energy to operate independently.
Two Terminals: The basic design allows it to be connected in various circuits.

Capacitance Formula

Capacitance (C) : $C = \frac{\varepsilon A}{d}$ $C = \frac{ε A}{d}$
- Where:
  - $C$ : Capacitance in Farads
  - $\varepsilon$ : Permittivity of the dielectric (absolute, not relative)
  - $A$ : Area of plate overlap in square meters
  - $d$ : Distance between plates in meters
- Ideas: Understanding this formula helps in selecting capacitors for specific applications, as it describes how the physical characteristics of the capacitor affect its ability to store charge.

Energy Stored

Energy (E) : $E = \frac{1}{2} C V^2$ $E = \frac{1}{2} C V^{2}$
- This shows how the energy stored in a capacitor is dependent on its capacitance and the voltage across it.
- Additional Information: The greater the capacitance and voltage, the more energy can be stored, which is vital in applications like power supply smoothing.

Voltage and Charge Relations

Basic Relationships:
- $Q = CV$
- $V = \frac{Q}{C}$

Symbol	Meaning
Q	Charge (Coulombs)
C	Capacitance (Farads)
V	Voltage (Volts)

Thoughts: These equations illustrate how charge, capacitance, and voltage are interrelated, allowing engineers to calculate one variable when the other two are known.

Reference:

courses.lumenlearning.com

Energy Stored in Capacitors | Physics - Courses.lumenlearning.com.

www.omnicalculator.com

Capacitor Energy Calculator

phys.libretexts.org

8.4: Energy Stored in a Capacitor - Physics LibreTexts

Types of Capacitors

Capacitors are essential components in electronic circuits, and they come in various types, each with distinct characteristics and applications. Here are some insights based on the image:

1. Tantalum Capacitors

Description: Tantalum capacitors are known for their high capacitance values and stability over a wide range of temperatures.
Thoughts: These capacitors are often used in applications where size and reliability are critical, such as in mobile devices and aerospace.
Additional Info: They have a higher cost compared to aluminum capacitors but offer better performance in many situations.

2. Aluminum Capacitors

Description: Aluminum capacitors are widely used due to their relatively low cost and good performance.
Thoughts: Their availability makes them a favorite for general-purpose applications, but they can be bulky compared to other types.
Additional Info: They may have a shorter lifespan than tantalum capacitors under certain conditions, particularly at high temperatures.

3. Ceramic Capacitors

Description: Ceramic capacitors are known for their small size and reliability, featuring a wide range of dielectric strengths.
Thoughts: They are commonly used in high-frequency applications, like RF circuits, because of their low Equivalent Series Resistance (ESR).
Additional Info: The capacitance value can change with applied voltage (voltage coefficient), which should be considered in design.

4. Trimmer Capacitors

Description: Trimmer capacitors are adjustable capacitors often used for tuning applications.
Thoughts: Their ability to be fine-tuned makes them essential in radio transmitters and receivers for precise frequency settings.
Additional Info: They are usually less common in general electrical applications but are critical in RF applications.

5. Thin Film Capacitors

Description: Thin film capacitors are characterized by their high precision and stability.
Thoughts: These capacitors are used in high-performance applications where tight tolerances are required, such as in precision measurement instruments.
Additional Info: They can be more expensive than other types due to their manufacturing process and material quality.

Summary of Capacitor Types

Type	Characteristics	Applications
Tantalum	High capacitance, stable across temperatures	Mobile devices, aerospace
Aluminum	Low cost, good performance, larger size	General-purpose applications
Ceramic	Small size, reliable, good for high frequencies	RF circuits
Trimmer	Adjustable, used for tuning	RF transmitters/receivers
Thin Film	High precision, stable	Precision measurement instruments

Understanding the various types of capacitors helps in selecting the right component for specific electronic applications, balancing factors like size, cost, and performance requirements.

Reference:

vitrek.com

Types of Capacitors | Capacitor Types by Function & Application

www.digikey.com

Understanding Capacitor Types and Characteristics | DigiKey

vitrek.com

Capacitor Characteristics and Applications | MTI Instruments - Vitrek

Inductor

Definition

An inductor, also known as a coil, choke, or reactor, is a two-terminal electrical component that stores energy in a magnetic field when electric current flows through it.
- Thoughts: Inductors are fundamental in controlling current in electrical circuits. Understanding their function is crucial for designing various electronic devices.

Structure

Typically consists of an insulated wire wound into a coil.
- Idea: The physical structure of the inductor, the coil, enhances its ability to store magnetic energy. The shape and materials used can significantly affect performance.

Inductance Formula

The inductance $L$ $L$ is given by the formula: $L = \frac{N^2 \mu A}{l}$ $L = \frac{N ^{2} μ A}{l}$ Where:
- $L$ = Inductance of coil in Henrys
- $N$ = Number of turns in wire coil (for a straight wire, $N = 1$ )
- $\mu$ = Permeability of core material (absolute, not relative)
- $\mu_r$ = Relative permeability (dimensionless, $\mu_0 = 1$ for air)
- $\mu_0 = 1.26 \times 10^{-6} \, \text{T·m/A}$ (permeability of free space)
- $A$ = Area of coil in square meters $= \pi r^2$
- $l$ = Average length of coil in meters
- Thoughts: This formula shows that inductance increases with the number of turns and the permeability of the core material, making material selection important in inductor design.

Self-Inductance Concept

Self-inductance refers to the property of an inductor that allows it to oppose changes in current flow through it.
- Additional Info: This property is vital in applications like transformers and energy storage devices, where maintaining a stable current is necessary.

Related Concepts

Lenz's Law: A fundamental principle that states that an induced electromotive force (EMF) will generate a current that opposes the change in magnetic flux that produced it.
- Insight: This concept is essential for understanding how inductors react in dynamic circuits and contributes to the design of more efficient electrical systems.

Key Concepts

Magnetic Field Relation:
- $B = \mu N \frac{I}{l}$ (Magnetic field strength)
- $E = -L \frac{dI}{dt}$ (Induced EMF)
- Thoughts: These equations further demonstrate the relationship between current, magnetic fields, and how inductors can control electrical energy flow. Understanding these relationships is crucial for anyone working with electrical circuits.

Reference:

Inductance - Wikipedia

Inductance of a Coil - Electronics Tutorials

phys.libretexts.org

14.3: Self-Inductance and Inductors - Physics LibreTexts

Mutual Inductance

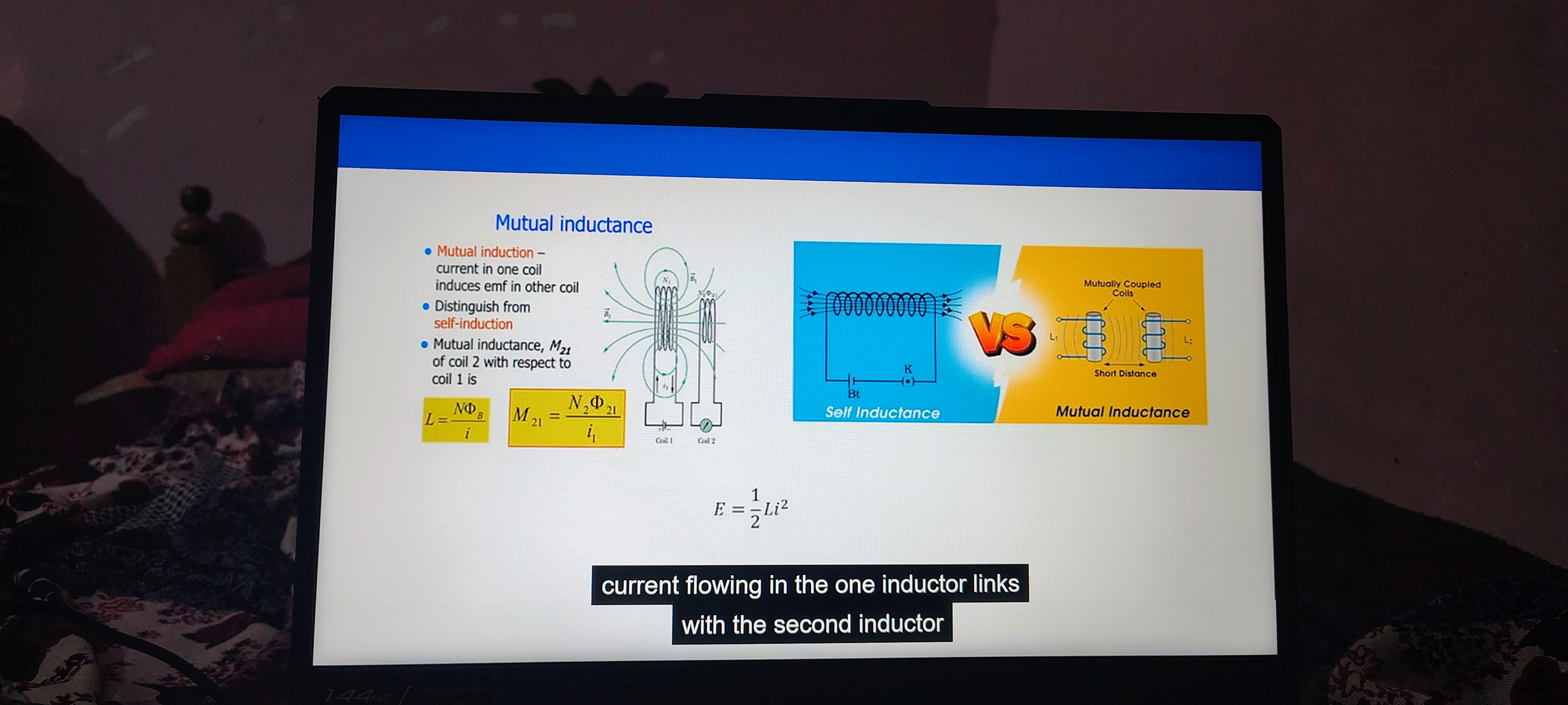
Key Concepts

Mutual Induction:
- Definition: This phenomenon occurs when the current flowing in one coil induces an electromotive force (emf) in another coil. It distinguishes from self-induction, where the induced emf is in the same coil.
- Thought: Mutual induction is essential in transformers and various electrical devices, as it allows energy transfer without direct electrical connection.
Distinction from Self-Induction:
- In self-induction, a single coil generates an emf due to its own changing current. In contrast, mutual induction involves two coils affecting each other through the magnetic field.
- Additional Info: While both phenomena involve inductance, their applications can vary significantly, like in inductors vs transformers.

Formulae

Mutual Inductance ( $M_{21}$ ) : $M_{21} = \frac{N_2 \Phi_{21}}{I_1}$ Where:
- $N_2$ = Number of turns in coil 2
- $\Phi_{21}$ = Magnetic flux linked with coil 2 due to the current in coil 1
- $I_1$ = Current in coil 1
General Inductance Formula: $L = \frac{N \Phi_B}{i}$ Where:
- $N$ = Number of turns
- $\Phi_B$ = Magnetic flux
- $i$ = Current
Energy Stored in Inductor: $E = \frac{1}{2} Li^2$
- Explanation: This formula indicates how much energy is stored in the inductor when a current flows through it. The energy is proportional to the square of the current and the inductance.

Illustrations

Self Inductance vs Mutual Inductance:
- Self Inductance: Represented as a single coil.
- Mutual Inductance: Shown with two coils that are closely coupled, demonstrating the interaction between them.
- Importance: Understanding these concepts is crucial for designing circuits and devices that utilize inductors efficiently.

Summary

Mutual inductance is a critical concept in electromagnetism that allows for energy transfer between coils via magnetic fields. Understanding its principles helps in grasping how transformers and inductive coupling work in electronic devices.

Reference:

byjus.com

Definition, Self Inductance, Mutual Inductance, Difference - BYJU'S

readingfeynman.org

Self-inductance, mutual inductance, and the power and energy of ...

www.youtube.com

01 - What is Mutual Inductance & Self Inductance in Circuit Analysis?

Resistor vs Capacitor vs Inductor

This document compares resistors, capacitors, and inductors, which are fundamental components in electrical circuits.

Elements	Resistor	Capacitor	Inductor
Symbol	R	C	L
Denoted by	R	C	L
Equation	$R = \frac{V}{I}$	$C = \frac{Q}{V}$	$L = \frac{V_L}{di/dt}$
Series	$R_T = R_1 + R_2$	$\frac{1}{C_T} = \frac{1}{C_1} + \frac{1}{C_2}$	$L_T = L_1 + L_2$
Parallel	$\frac{1}{R_T} = \frac{1}{R_1} + \frac{1}{R_2}$	$C_T = C_1 + C_2$	$\frac{1}{L_T} = \frac{1}{L_1} + \frac{1}{L_2}$

Notes:

Resistor:
- Function: Resistors limit current flow and voltage in a circuit. They convert electrical energy into heat, which is why they get warm.
- Application: Used to control the current in various circuits, such as voltage dividers and pull-up resistors.
Capacitor:
- Function: Capacitors store and release electrical energy. They can smooth out fluctuations in voltage.
- Application: Commonly used in filtering applications (e.g., smoothing power supply outputs) and tuning circuits (e.g., radio frequency circuits).
Inductor:
- Function: Inductors store energy in a magnetic field when electrical current flows through them. They resist changes in current.
- Application: Used in filters, transformers, and energy storage in power supplies, often in conjunction with capacitors to create oscillatory circuits.

Summary of Equations:

Ohm's Law for Resistors: This defines the relationship between voltage, current, and resistance.
Capacitance Relationship: Describes how the capacitance value changes when capacitors are arranged in series or parallel.
Inductance Relationship: Similar to capacitance, the inductance changes depending on how inductors are configured in the circuit.

Understanding these components and their equations is essential for designing and troubleshooting electrical and electronic systems.

Reference:

app.jove.com

RC/RL/LC Circuits - JoVE

www.ducksters.com

Resistors, Capacitors, and Inductors - Physics for Kids - Ducksters

www.vedantu.com

Capacitor Inductor Resistor : Learn Definition, Uses & Examples

Notes on Electrical Inductance Quiz

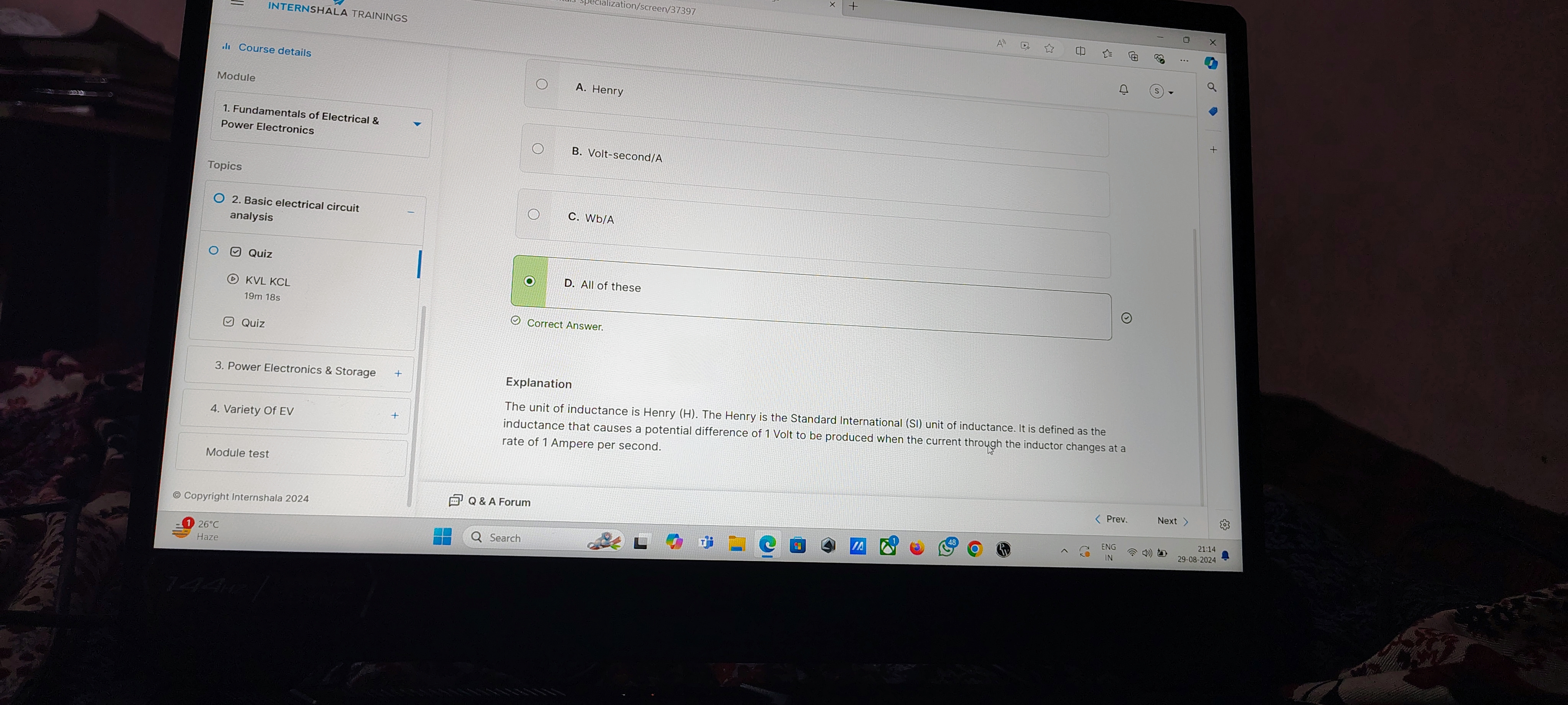
Key Concepts

Unit of Inductance: Henry (H)
- The basic unit of inductance in the International System of Units (SI) is Henry, symbolized as 'H'.
- Inductance is crucial in electrical circuits, as it relates to how the circuit responds to changes in current.

Explanation of Henry:

Definition:
- The Henry is defined as the inductance that causes a potential difference of 1 Volt to be produced when the current through the inductor changes at a rate of 1 Ampere per second.
- This definition underscores the relationship between voltage, current, and time in magnetic fields and inductors.

Quiz Content:

Question: What is the unit of inductance?
- Options:
  - A. Henry
  - B. Volt-second/A
  - C. Wb/A
  - D. All of these
- Correct Answer: D. All of these
  - Thoughts: This highlights that various expressions can describe the same physical quantity, emphasizing the interconnectedness of electrical units. Understanding these different terms can aid in clearer communication in electrical engineering.

Additional Information:

Inductance in Circuits:
- Inductance is a fundamental property for components like inductors in circuits, used in filters, transformers, and energy storage elements.
Applications:
- Knowledge of inductance is essential for designing circuits that control currents, such as in power supplies, radios, and more advanced electronic devices.

Summary:

Understanding the unit of inductance and its applications is critical for anyone studying electrical engineering or involved in designing electrical circuits. The quiz format encourages active recall, aiding comprehension of foundational concepts in electronics.

Reference:

library.fiveable.me

Henry - Vocab, Definition, and Must Know Facts | Fiveable

quizlet.com

Electrical Engineering 2 Flashcards | Quizlet

forums.mikeholt.com

Exam Question - Mike Holt's Forum

Kirchhoff's Laws

Kirchhoff's Laws Overview

Definition: Kirchhoff's laws are fundamental principles in electrical engineering that help analyze complex electric circuits.
Components: These laws are divided into two main categories:
- Voltage Law (KVL) : This law states that the total voltage around any closed loop in a circuit is equal to zero. It emphasizes the conservation of energy within circuits, ensuring that all voltages rise and drop in a loop balance out.
- Current Law (KCL) : According to this law, the total current entering a junction must equal the total current leaving that junction. This reflects the conservation of charge in electrical circuits.

Key Points

Application: Kirchhoff's laws are used to find voltage and current in circuits that contain multiple components. They are essential for both AC (Alternating Current) and DC (Direct Current) circuit analysis.
Equivalent Resistance: Using Kirchhoff's laws, engineers can simplify the process of finding the equivalent resistance of complex networks. This is crucial for efficiently designing circuits.
Simplification of Circuits: Both AC and DC circuits can be simplified through the application of these laws, making analysis more manageable.

By understanding these laws, one can effectively troubleshoot and design electrical circuits, ensuring they operate efficiently and safely.

Reference:

www.youtube.com

Circuit Analysis Using Kirchhoff's Current & Voltage Laws - YouTube

phys.libretexts.org

10.4: Kirchhoff's Rules - Physics LibreTexts

engineering.louisville.edu

Lesson 3. Circuit Solving with Kirchhoff's Laws

Circuit Definitions

Key Terms

Term	Definition
Branch	A circuit single element
Node	It is a point of connection for two or more branches
Loop	Any closed path in a circuit
Network	Interconnection of elements or devices
Circuit	A network providing one or more closed paths

Notes and Additional Information

Branch:
- Each branch in an electrical circuit typically contains a component, such as resistors, capacitors, or inductors. Understanding branches is essential for analyzing how current flows through a circuit and how voltage is distributed.
Node:
- Nodes serve as junction points where two or more branches meet. Knowing how many branches connect at a node helps in applying Kirchhoff's laws, which are fundamental for circuit analysis.
Loop:
- A loop is formed when you can traverse a complete path in a circuit without lifting your pencil from the paper and returning to the starting point. Analyzing loops is vital for calculating currents and voltages in complex circuits using techniques like mesh analysis.
Network:
- A network refers to the overall configuration of elements within the circuit, including connections, branches, and nodes. The concept of networks is vital in systems like communications and power distribution.
Circuit:
- This term encompasses the whole system defined by its nodes, branches, and loops. Understanding circuits as networks with closed paths is crucial for designing and troubleshooting electronic systems, as well as for implementing various circuit theorems.

Diagram Insights

The diagram in the image visualizes a basic circuit with nodes labeled A, B, and C, along with resistors and loops. This visual representation aids in illustrating how branches and loops function within a network, emphasizing the practical aspect of circuit theory.

Reference:

www.doe.carleton.ca

5 nodes 9 loops 8 branches - +

electrical-engineering-portal.com

Electric Circuits? It's All About Nodes, Branches, and Loops

www.electrical4u.com

Nodes, Branches and Loops of a Circuit - Electrical4U

Kirchhoff’s Current Law (KCL)

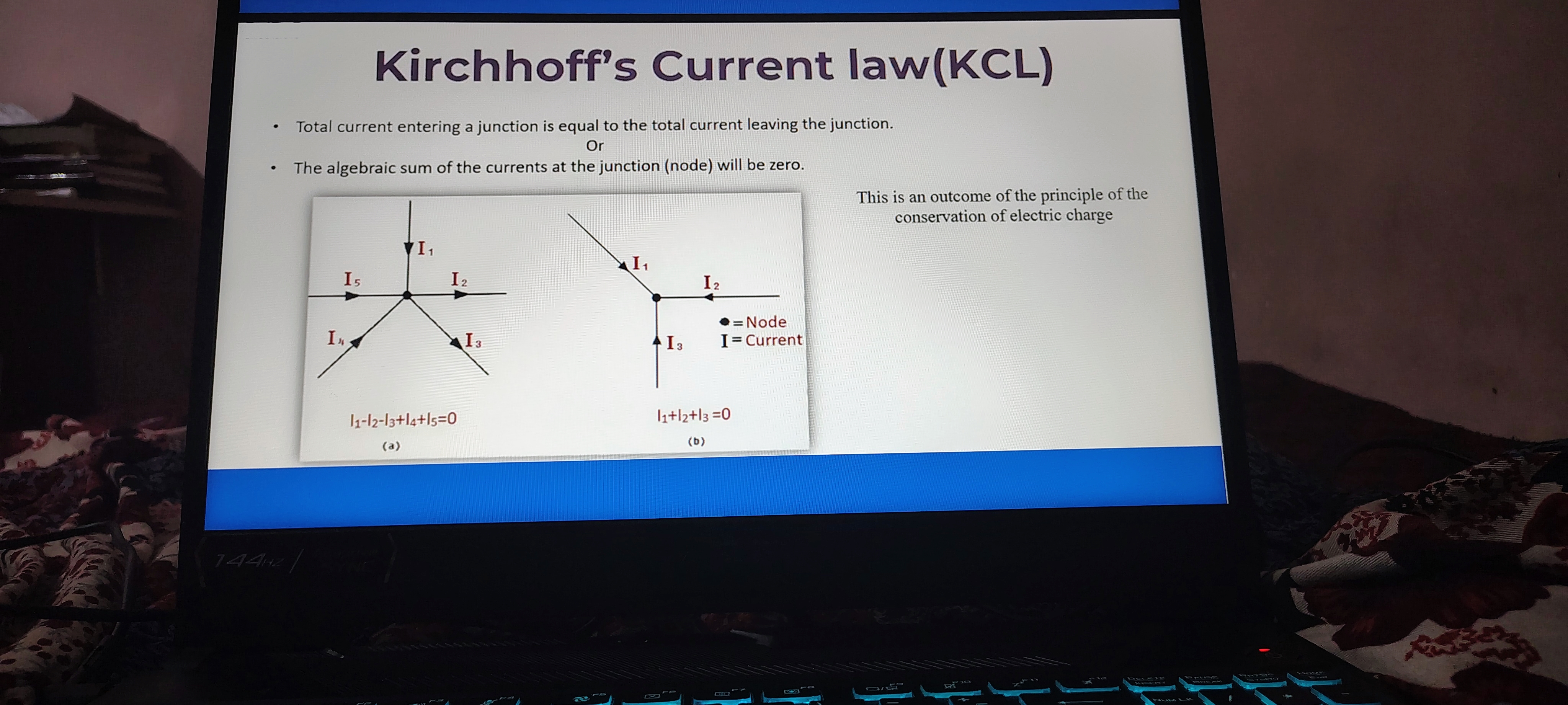
Total Current at a Junction: The total current entering a junction is equal to the total current leaving the junction.
- Thought: This principle is crucial in circuit analysis since it helps to maintain the balance of electrical charge. Understanding how current behaves at junctions allows engineers to design more efficient circuits.
Algebraic Sum of Currents: The algebraic sum of the currents at the junction (node) will be zero.
- Additional Information: If we label incoming currents as positive and outgoing currents as negative, this principle can be expressed mathematically as: $I_1 + I_2 + I_3 + I_4 + I_5 = 0$ where currents entering the node are considered positive and those leaving it are negative.
Example Equations:
1. From the first diagram: $I_1 - I_2 - I_3 + I_4 + I_5 = 0$
2. From the second diagram: $I_1 + I_2 + I_3 = 0$
- Thought: These equations exemplify how KCL is applied in circuit analysis. They can help in determining the unknown currents when some values are known.
Conservation of Electric Charge: KCL stems from the principle of conservation of electric charge.
- Additional Information: This means that charge cannot be created or destroyed in an isolated system; it can only flow from one part of the circuit to another. This fundamental concept underlies all electrical engineering and physics.

Visual Representation:

Diagrams provided illustrate currents ( $I_1, I_2, I_3, I_4, I_5$ ) at various junctions and how they interact according to KCL principles.

Reference:

Kirchhoff's Current Law, (KCL) and Junction Rule

www.keysight.com

Kirchhoff's Current Law Simplified: The Engineer's Guide - Keysight

openstax.org

21.3 Kirchhoff's Rules - College Physics 2e | OpenStax

Kirchhoff's Voltage Law

Definition: Kirchhoff's Voltage Law (KVL) states that the algebraic sum of voltage drops in a closed loop is zero.
- Thoughts: This principle is fundamental in circuit analysis, as it helps in understanding how voltages behave in electrical circuits. It's a direct consequence of the conservation of energy, emphasizing that energy supplied in a loop must equal the energy used.
Application: The algebraic sum of the EMF (Electromotive Force) applied is equal to the algebraic sum of the voltage drops in the elements of the circuit.
- Additional Information: EMF can be thought of as the total voltage provided by a power source like a battery. Each component in a circuit, such as resistors, creates a voltage drop that must be accounted for when applying KVL.
Importance of Direction: It's crucial to determine the direction of current when solving circuits using Kirchhoff’s laws.
- Thoughts: The current direction significantly affects voltage drops across components. Correctly understanding current flow helps in accurately applying KVL and obtaining the correct values.
Conservation of Energy: This idea is intrinsic to KVL, reflecting the conservation of energy within electrical systems.
- Additional Information: Like energy cannot be created or destroyed, in a closed electrical circuit, the total energy supplied must be equal to the total energy consumed.

Example Circuit Analysis

Component	Resistance (R)	Voltage (V)
R1	5 kΩ	-
R2	10 kΩ	-
R3	7.5 kΩ	-
Total	-	45 V

Equation Breakdown:
- $45 = R_1 + R_2 + R_3$
- $45 = 5 + 10 + 7.5$
- This equation illustrates how the sum of voltage drops across all resistors equals the supplied voltage, reinforcing KVL principles.

Key Takeaways

KVL is essential for solving complex circuits.
Correct understanding of voltage drops and currents leads to accurate circuit analysis.
The principle underpins much of electronic design and troubleshooting.

Reference:

Kirchhoff's Voltage Law and the Conservation of Energy

www.keysight.com

Engineer's Guide: Conquer Kirchhoff's Voltage Law in Simple Steps

www.albert.io

Kirchhoff's Circuit Laws | Explanation and Review - Albert.io

Circuit Analysis Example

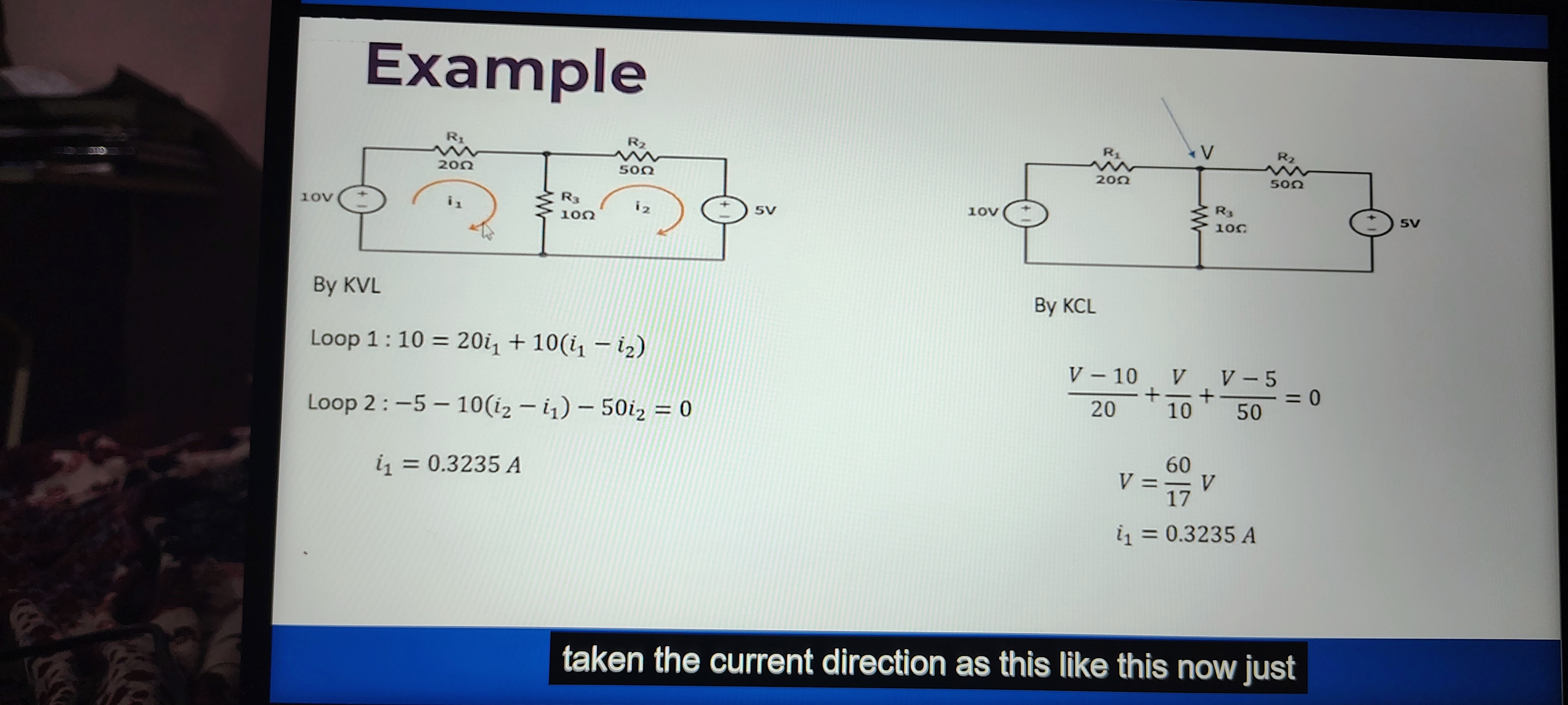
Overview

This image discusses the analysis of an electrical circuit using Kirchhoff's Voltage Law (KVL) and Kirchhoff's Current Law (KCL). The circuit consists of resistors and voltage sources, and it uses loop equations to find the current values.

Key Points

Kirchhoff's Voltage Law (KVL) :
- KVL states that the sum of all electrical potential differences (voltage) around any closed circuit loop must equal zero. This principle is fundamental in circuit analysis.
- In this example, two loops are analyzed:
  - Loop 1 Equation: $10 = 20i_1 + 10(i_1 - i_2)$ $10 = 20 i_{1} + 10 (i_{1} - i_{2})$
    - This equation represents the voltage drop around Loop 1, accounting for the voltage source and the resistive elements.
  - Loop 2 Equation: $-5 - 10(i_2 - i_1) - 50i_2 = 0$ $- 5 - 10 (i_{2} - i_{1}) - 50 i_{2} = 0$
    - This equation represents Loop 2, ensuring that the voltage drops equals the voltage rises.
Kirchhoff's Current Law (KCL) :
- KCL states that the sum of currents entering a junction must equal the sum of currents leaving that junction.
- The equation derived from KCL in this example helps in determining the voltage $V$ : $\frac{V - 10}{20} + \frac{V}{10} + \frac{V - 5}{50} = 0$
- This equation allows the calculation of $V$ based on the resistor values and voltage sources.
Current Values:
- The calculated current $i_1$ is $0.3235 \, A$ .
- This indicates the amount of current flowing through the specified branch of the circuit.

Tables

Component	Values
Resistor R1	20 Ω
Resistor R2	50 Ω
Resistor R3	10 Ω
Voltage Source 1	10 V
Voltage Source 2	5 V
Calculated $i_1$	0.3235 A

Additional Thoughts

Understanding KVL and KCL is crucial for analyzing electrical circuits effectively. These laws are not just theoretical; they form the basis for many practical applications, including circuit design and troubleshooting. It is beneficial for students to practice various circuit configurations using these laws to solidify their comprehension.

Reference: