Simple Linear Regression: Theory and Computation Guide

ML BASICS - SIMPLE LINEAR REGRESSION THEORY

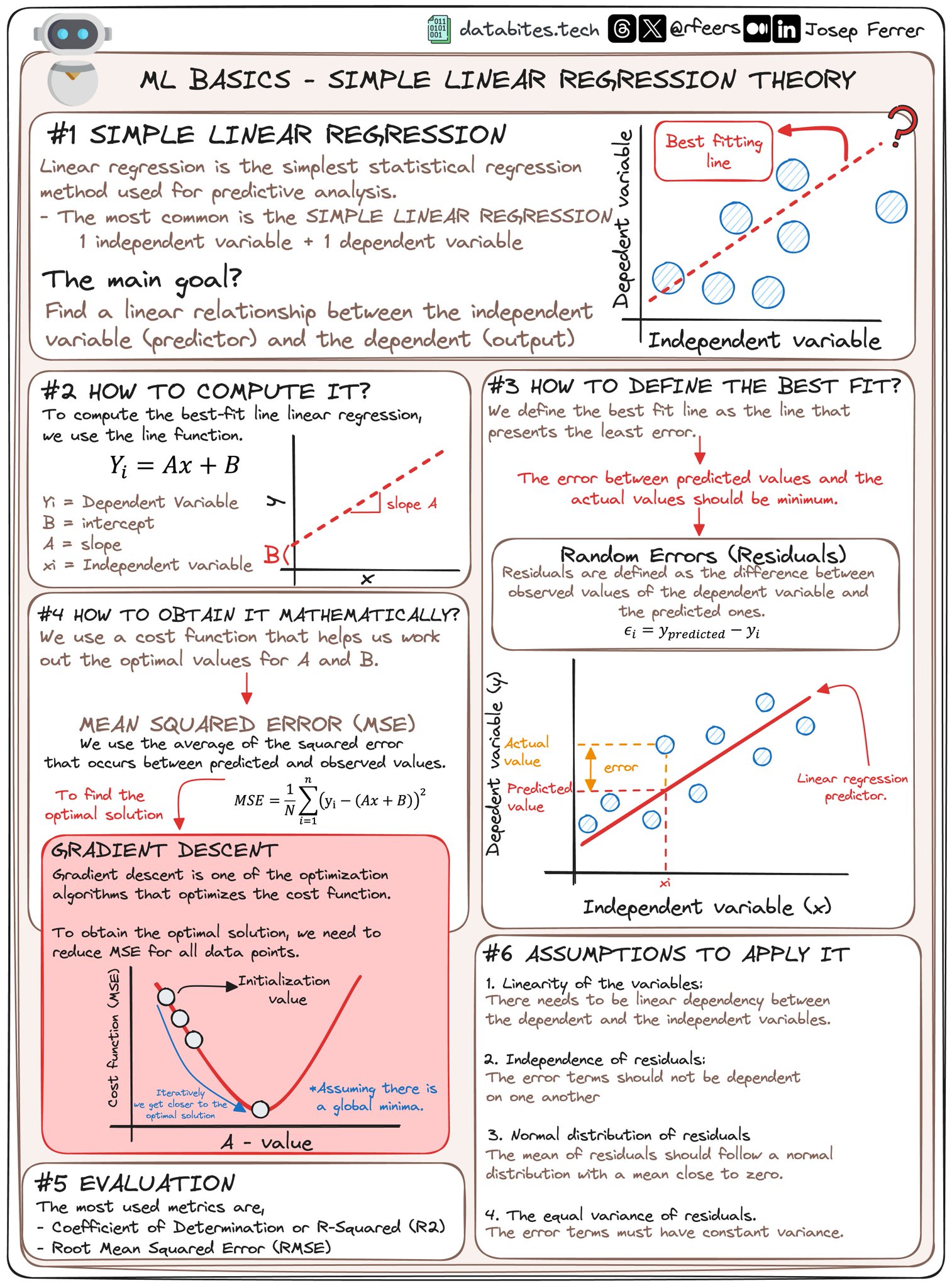
1. SIMPLE LINEAR REGRESSION

Linear regression is the simplest statistical regression method used for predictive analysis.

• The most common is the SIMPLE LINEAR REGRESSION with 1 independent variable + 1 dependent variable.

The main goal: Find a linear relationship between the independent variable (predictor) and the dependent (output).

Explanation: Simple linear regression aims to model the relationship between a scalar response (dependent variable y) and a scalar predictor (independent variable x). It attempts to draw the best fitting straight line through the data points.

2. HOW TO COMPUTE IT?

To compute the best-fit line linear regression, we use the line function: [ Y_{i} = Ax + B ]

• (Y_{i}) = Dependent Variable
• (B) = intercept
• (A) = slope
• (x_{i}) = Independent variable

Explanation: This linear equation defines a straight line where (A) is the slope, and (B) is the y-intercept. We adjust (A) and (B) to get the closest possible fit to the data points.

3. HOW TO DEFINE THE BEST FIT?

We define the best fit line as the line that presents the least error. The error between predicted values and the actual values should be minimum.

Explanation: The best-fit line minimizes the differences between predicted values and observed data points. This is often visualized via a scatter plot with the line of best fit drawn through the data points.

Random Errors (Residuals)

Residuals are defined as the differences between observed values of the dependent variable and the predicted ones. [ \epsilon_{i} = y_{predicted} - Y_{i} ]

Explanation: Residuals measure how far away each data point is from the regression line. They are crucial for evaluating the performance and accuracy of the regression model.

4. HOW TO OBTAIN IT MATHEMATICALLY?

We use a cost function that helps us work out the optimal values for A and B.

MEAN SQUARED ERROR (MSE)

We use the average of the squared error that occurs between predicted and observed values. [ MSE = \frac{1}{N} \sum_{i=1}^{N} (Y_{i} - (Ax + B))^{2} ] To find the optimal solution: [ Gradient Descent ]

Explanation: MSE is a common measure for the accuracy of a regression model—it calculates the average of the squares of the errors. Finding the minimum MSE is essential to determine the best possible values for (A) and (B).

GRADIENT DESCENT

Gradient descent is one of the optimization algorithms that optimizes the cost function.

• To obtain the optimal solution, we need to reduce MSE for all data points.
• Iteratively get closer to the optimal values.

Explanation: Gradient descent is an iterative optimization algorithm used to minimize the MSE by moving in the direction of the steepest descent as defined by the negative gradient.

5. EVALUATION

The most used metrics are:

• Coefficient of Determination or R-Squared ((R^{2}))
• Root Mean Squared Error (RMSE)

Explanation: Evaluating the model involves checking how well it performs on unseen data. The Coefficient of Determination (R-squared) shows the proportion of the variance in the dependent variable predictable from the independent variable. RMSE measures the average magnitude of the errors.

6. ASSUMPTIONS TO APPLY IT

1. Linearity of the variables: There needs to be linear dependency between the dependent and the independent variables.
2. Independence of residuals: The error terms should not be dependent on one another.
3. Normal distribution of residuals: The mean of residuals should follow a normal distribution with a mean close to zero.
4. The equal variance of residuals: The error terms must have constant variance.

Explanation: These assumptions are necessary to validate the model. Linearity ensures the relationship can be modeled accurately by a straight line. Independence and normal distribution ensure that the residuals do not have any patterns and equal variance ensures homoscedasticity.

Reference: