Vector Spaces: Basics and Key Concepts in Linear Algebra

Vector Spaces

Table of Contents

• 1.1 Introduction
• 1.2 Vector Spaces
• 1.3 Subspaces
• 1.4 Linear Combinations and Systems of Linear Equations
• 1.5 Linear Dependence and Linear Independence
• 1.6 Bases and Dimension
• 1.7* Maximal Linearly Independent Subsets

1.1 Introduction

• ** Vectors in Physics**
  • Concepts such as forces, velocities, and accelerations are vectors.
  • Vectors have both magnitude and direction, essential for describing physical phenomena.
  • A vector is represented by an arrow, where the length represents magnitude and the arrowhead indicates direction.
  • ** Insight**: Understanding the vector quantities helps in analyzing physical systems and predicting outcomes.
• ** Vector Equivalence**
  • Vectors with the same magnitude and direction are considered equal, regardless of position.
  • ** Idea**: This property is especially useful in physics, where vectors can be moved parallel in space without altering physical meaning.
• ** Vector Addition**
  • When two vectors act simultaneously, their effects combine.
  • ** Example**: A swimmer moving against a river current sees a net reduction in speed, while moving with the current sees an increase.
  • ** Insight**: This demonstrates how vectors influence each other based on direction and magnitude.

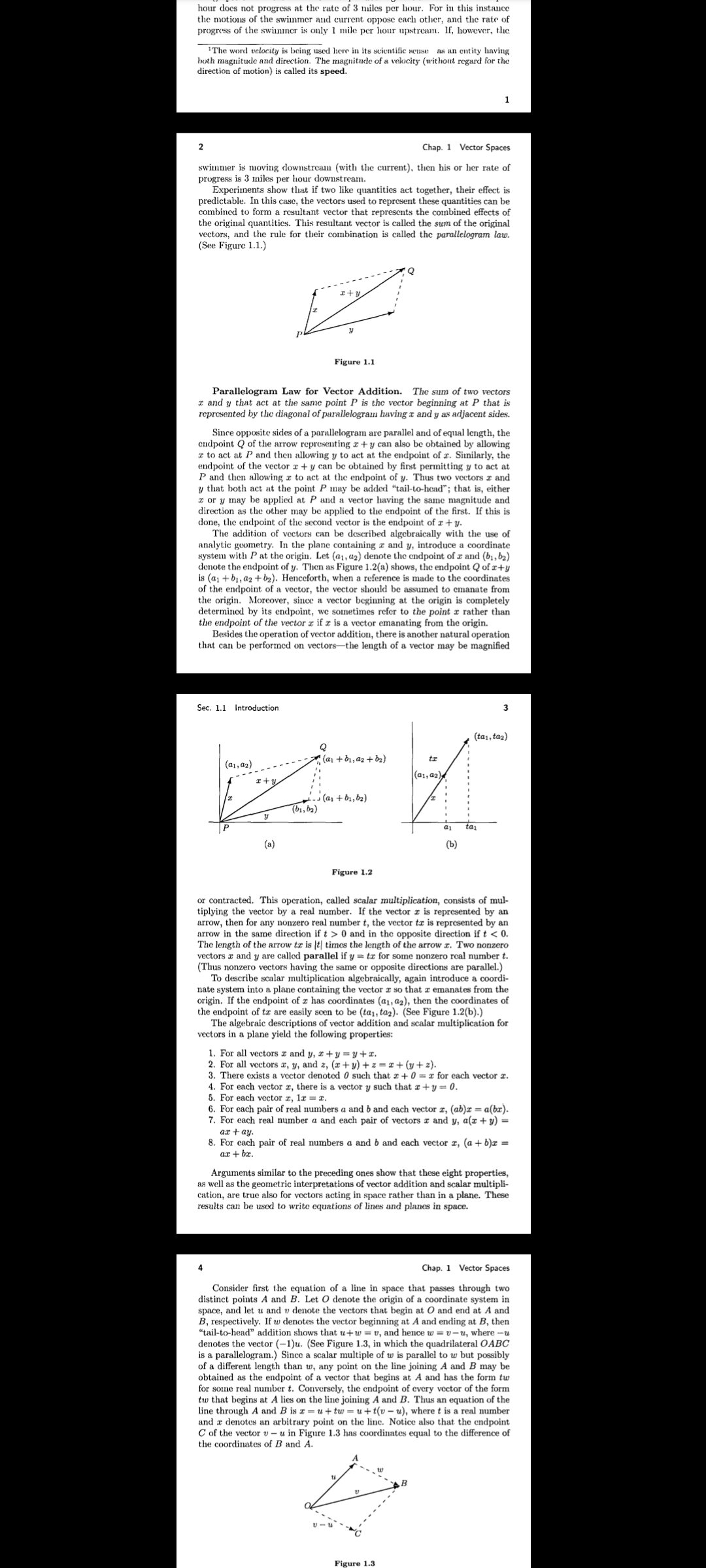
Parallelogram Law for Vector Addition

• ** Definition**
  • The sum of two vectors $x$ and $y$ is the vector represented by the diagonal of the parallelogram formed by placing $x$ and $y$ tail-to-tail.
  • ** Insight**: This law is foundational for understanding vector addition; useful for graphical interpretation and calculation.
• ** Process**
  • Vectors can be added by placing them "tail-to-head" and forming a parallelogram.
  • ** Additional Information**: This method visualizes vector addition in two dimensions and explains the resultant vector's position and length.
• ** Figure 1.1**
  • Demonstrates vector addition using the parallelogram law.
  • ** Extra Note**: Diagrammatic representation helps in visualizing and solving vector problems easily.

In these notes, understanding the basic properties and operations of vectors lays a fundamental base for analyzing complex systems in various scientific and engineering fields. Vectors provide a succinct way to represent and compute multidimensional quantities effectively.

Extended readings:

Vector Spaces: Key Concepts and Properties

Introduction to Vectors

• Vectors are mathematical entities with both direction and magnitude, commonly used in physics and engineering to represent quantities like velocity and force.

Velocity Context

• Velocity: A vector quantity involving both speed and direction, differing from scalar speed which is only magnitude.
  • Example: A swimmer’s net progress in water combines the velocity of swimming and water current.

Vector Addition

• Parallelogram Law: The vector addition rule where the sum of two vectors is represented by the diagonal of a parallelogram formed with the two vectors as adjacent sides.
  • Insight: Visualizing vector addition helps understand resultant forces and motion in physics.
• Coordinates and Vectors:
  • Denote endpoint positions with coordinates, i.e., vector $x$ with endpoint $(a_1, a_2)$.
  • Resultant Vector: If vector $x$ joins $y$, then resultant $z = x + y$ can be represented as $(a_1 + b_1, a_2 + b_2)$.

Scalar Multiplication

• Operation involving multiplying a vector by a real number, scaling its magnitude.
  • Expressing with Coordinates: For vector $z = (a_1, a_2)$, scalar multiplication like $tz = (ta_1, ta_2)$.

Properties of Vector Addition and Scalar Multiplication

1. Commutative & Associative Properties:

   • $x + y = y + x$
   • $(x + y) + z = x + (y + z)$

2. Existence of Zero Vector:

   • Unique vector $0$, such that $x + 0 = x$.

3. Existence of Additive Inverses:

   • For each $x$, there exists $-x$ such that $x + (-x) = 0$.

4. Scalar Operations:

   • Identity: $1x = x$.
   • Distributive Properties:
     • $a(x + y) = ax + ay$
     • $(a + b)x = ax + bx$

Application: Line Equation in Space

• Vector Formulation of Line:
  • For line through points A and B, where O is the origin, express as $u = \overrightarrow{OA}, v = \overrightarrow{OB}$.
  • Line Representation: Any point on line segment AB can be represented using vector linear combination.

Geometric Representation

• Figures and Diagrams:
  • Figures illustrate spatial conception of vector addition, scalar application, and line equations, aiding visual understanding.

These notes cover foundational aspects of vector spaces crucial for spatial and physical analysis, emphasizing understanding through visualization and algebraic manipulation. Explore further with linear algebra for deeper mathematical insights and applications.

Extended readings:

Vector Concepts and Linear Equations in Space

Vectors and Lines

• Vector Definition: Vectors are quantities having both magnitude and direction. They are often represented as directed line segments.

• Vector Components:

  • $\mathbf{w}$ and $\mathbf{v}$ : Given vectors $\mathbf{w}$ and $\mathbf{v}$, the vector $\mathbf{v} - \mathbf{u}$ is the difference between the two vectors. This difference forms another vector pointing from one endpoint to another.
  • Scalar Multiplication: A scalar multiple of a vector is parallel to the original vector but may have a different length.

• Line Equations:

  • A point $\mathbf{x}$, on the line through points $A$ and $B$, is given by: $\mathbf{x} = \mathbf{u} + t(\mathbf{v} - \mathbf{u}), \quad \text{where } t \text{ is a real number}$

Examples

Example 1

• Line Through Points:
  • Points $A$ and $B$ with coordinates $(-2, 0, 1)$ and $(4, 5, 3)$.
  • Vector $\mathbf{v} - \mathbf{u}$ is calculated as: $(4, 5, 3) - (-2, 0, 1) = (6, 5, 2)$
  • Equation of the line is: $\mathbf{x} = (-2, 0, 1) + t(6, 5, 2)$

Example 2

• Plane Through Points:
  • Points $A, B, C$ with coordinates $(1, 0, 2)$, $(-3, -2, 4)$, $(1, 8, -5)$.
  • Vector from $A$ to $B$: $(-3, -2, 4) - (1, 0, 2) = (-4, -2, 2)$
  • Calculating for $A$ to $C$: $(1, 8, -5) - (1, 0, 2) = (0, 8, -7)$
  • Plane equation is: $\mathbf{x} = (1, 0, 2) + s(-4, -2, 2) + t(0, 8, -7)$

Insights and Additional Information

• Points, Lines, and Planes: In three-dimensional space, two points determine a line, and three non-collinear points determine a plane.

• Parametric Equations: The parametric form allows expressing the location of any point on a line or plane using parameters that represent scalar multipliers for direction vectors.

• Geometric Interpretation: Understanding the geometric relationship between vectors, lines, and planes enhances spatial reasoning in fields like physics and engineering.

This section emphasizes the algebraic translation of geometric constructs into coordinate systems using vectors, crucial for vector analysis and modeling in various scientific domains.

Extended readings: