Distance Metrics in Data Science: Overview and Usage

Distance Metrics in Data Science

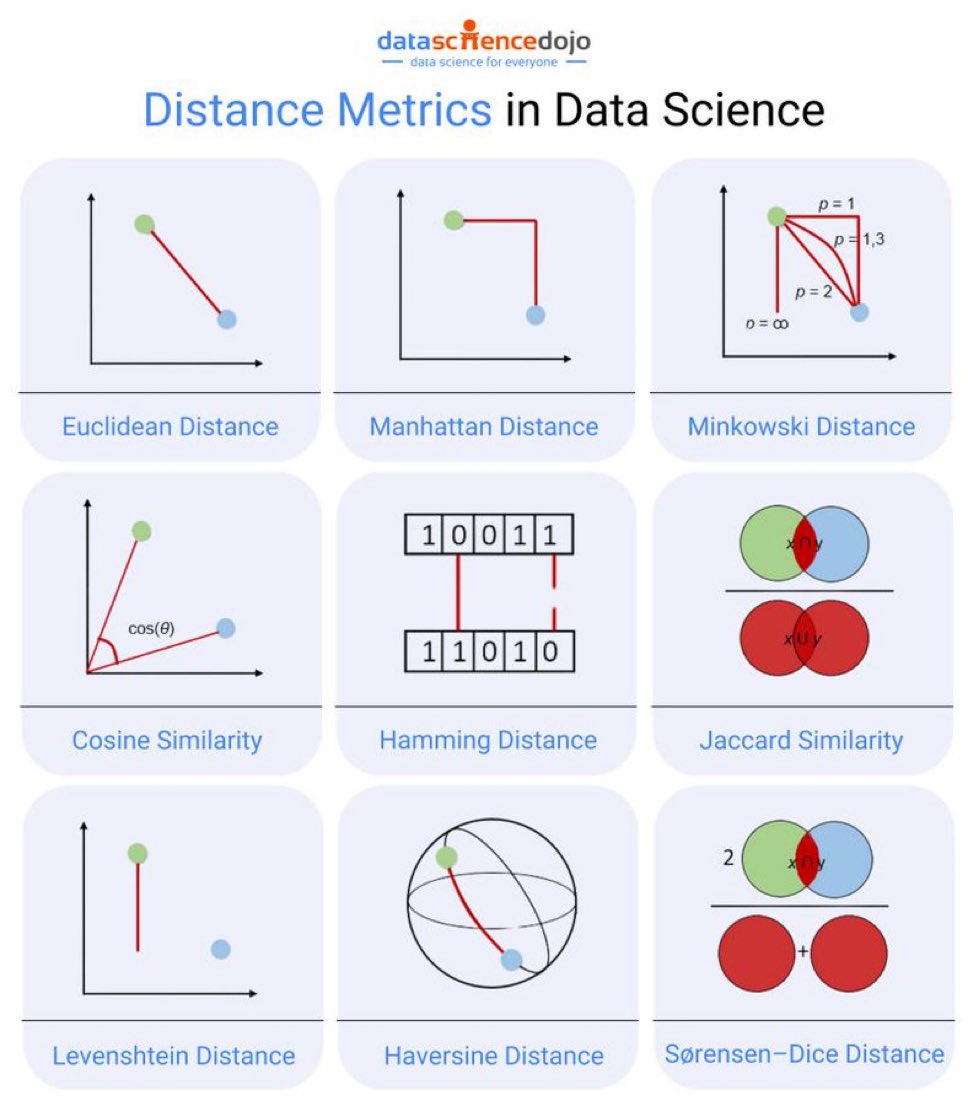
Euclidean Distance

• Description: Measures the straight-line distance between two points in Euclidean space.
• Formula: (\sqrt{\sum_{i=1}^{n} (x_i - y_i)^2})
• Usage: Commonly used in tasks requiring measurement of similarity between data points such as clustering and classification.

Manhattan Distance

• Description: Measures distance between two points along axes at right angles. Also known as L1 norm or taxicab distance.
• Formula: (\sum_{i=1}^{n} |x_i - y_i|)
• Usage: Useful in grid-based pathfinding algorithms and when differences in individual dimensions need equal treatment.

Minkowski Distance

• Description: Generalization of both Euclidean and Manhattan distance.
• Formula: ( \left(\sum_{i=1}^{n} |x_i - y_i|^p\right)^{1/p} )
• Parameter: ( p )
  • ( p = 1 ): Manhattan distance
  • ( p = 2 ): Euclidean distance
• Usage: Offers flexibility with ( p ) parameter, useful when specific dimensional contributions need to be balanced.

Cosine Similarity

• Description: Measures the cosine of the angle between two non-zero vectors. Values range from -1 to 1.
• Formula: ( \cos(\theta) = \frac{A \cdot B}{|A| |B|} )
• Usage: Useful for text analysis, comparing document similarity, and situations where magnitude differs.

Hamming Distance

• Description: Counts the number of positions at which corresponding elements differ. Primarily used for binary strings.
• Formula: ( Hamming(A, B) )
• Usage: Error detection and correction in data transmission, binary string comparison.

Jaccard Similarity

• Description: Measures similarity between finite sets by comparing the ratio of intersecting elements to the union of elements.
• Formula: ( J(A, B) = \frac{|A \cap B|}{|A \cup B|} )
• Usage: Used in clustering and information retrieval, especially in comparing sets or binary attributes.

Levenshtein Distance

• Description: Measures the minimum number of single-character edits required to change one word into another.
• Formula: ( Levenshtein(A, B) )
• Usage: Commonly used in text processing, spell checking, and plagiarism detection.

Haversine Distance

• Description: Measures the distance between points on the surface of a sphere. Essential for calculating great-circle distances.
• Formula: Involves spherical trigonometry.
• Usage: Ideal for geographic information systems (GIS) and applications involving global positioning.

Sørensen–Dice Distance

• Description: Measures the similarity between two samples. Similar to Jaccard Similarity but doubles the weight of intersection.
• Formula: ( \frac{2 |A \cap B|}{|A| + |B|} )
• Usage: Effective in ecology, biology, and other fields requiring robust similarity measurement between sets.

Reference: